
지난 포스트에서는 온라인 가중치 이분 매칭(online weighted bipartite matching)에 대해서 알아 보았습니다. 이 문제에서는 택시에 대한 정보는 미리 알고 있으며, 승객의 정보는 시간이 흐르면서 한 명씩 들어옵니다. 매 순간 어떤 승객의 정보가 알려질 때마다 우리는 이 승객을 택시에 할당할지 말지를 결정해야 하며, 만약 할당한다면 어느 택시에 태울지도 결정해야 합니다. 지난 포스트에서는 언젠가 승객을 어떤 택시에 할당했을 때 이를 더이상 번복할 수 없다면 좋은 경쟁비(competitive ratio)를 얻을 수 없다는 것을 확인하였습니다. 자세한 사항은 이전 포스트를 참고하시기 바랍니다.
2021.02.14 - [온라인 알고리즘/Online matching] - 온라인 가중치 이분 매칭 (Online Weighted Bipartite Matching)
온라인 가중치 이분 매칭 (Online Weighted Bipartite Matching)
저번 글에서는 온라인 이분 매칭 문제(online bipartite matching problem)가 무엇인지 설명하고 이를 경쟁적으로 해결하는 알고리즘에 대해서 알아 보았습니다. 문제를 간략히 다시 소개하도록 하겠습니
gazelle-and-cs.tistory.com
어떤 문제가 이론적으로 어려운 경우에 많이 하는 작업은 문제의 입력에 특정한 조건을 추가하는 것입니다. 조건이 추가되면 몇몇 어려운 입력들을 고려하지 않을 수 있게 되므로 문제의 난이도가 감소하는 효과를 얻습니다. 이번 글에서는 가중치에 조건을 추가해 보도록 하겠습니다. 이론적으로도 흥미롭고 실생활에서도 유용한 수많은 조건이 있지만, 그중에서도 보편적으로 활용되는 삼각 부등식(triangle inequality)을 고려하고자 합니다.
임의의 서로 다른 세 지점 \( u, v, w \)에 대해서 \(u\)와 \(v\) 사이의 가중치가 \(u\)와 \(w\), \(w\)와 \(v\) 사이 각각의 가중치의 합을 더한 것보다 길지 않을 때 우리는 해당 가중치가 삼각 부등식을 만족한다고 말합니다. 이는 실생활에서 거리(distance)에 대응하여 생각하면 편합니다. 한 지점에서 다른 지점으로 곧장 향하는 거리는 다른 곳을 경유하여 가는 거리보다 길지 않을 것으로 가정하여도 괜찮겠죠. 따라서 아래에서는 가중치라는 표현 대신 거리라는 표현을 사용하도록 하겠습니다.
지난 포스트에서와 같이 아래에서는 최소 거리 완벽 매칭(minimum-distance perfect matching)과 최대 거리 완벽 매칭(maximum-distance perfect matching)을 고민해 보겠습니다. 본문의 내용을 요약하면 다음과 같습니다.
- 최소 거리 완벽 매칭에서 매번 할당 가능한 택시 중 가장 가까운 택시에 할당하는 알고리즘은 지수적으로(exponentially) 못한다. 다행히도 선형적인(linear) 경쟁비를 갖는 알고리즘이 존재하며, 이는 결정론적 알고리즘(deterministic algorithm)으로 달성할 수 있는 점근적으로 최선(asymptotically best-possible)의 방법이다.
- 최대 거리 완벽 매칭에서 매번 할당 가능한 택시 중 가장 먼 택시에 할당하는 알고리즘은 \(\frac{1}{3}\)의 경쟁비를 가지며, 이는 결정론적 알고리즘으로 달성할 수 있는 최선의 방법이다.
최소 거리 완벽 매칭
문제를 엄밀히 정의하겠습니다. 입력으로는 어떤 완전 이분 그래프(complete bipartite graph) \( G = (L \cup R, E) \)와 간선 위의 거리 \( d : E \to \mathbb{Q}_+ \)가 주어집니다. 이때 \(d\)는 삼각 부등식을 만족합니다. 즉, 임의의 서로 다른 세 지점 \( u, v, w \in L \cup R \)에 대해, \[ d(u, v) \leq d(u, w) + d(w, v) \]를 만족합니다. 우리의 목표는 완벽 매칭을 찾는 것이므로 \( n := |L| = |R| \)이라고 가정하겠습니다.
이전과 마찬가지로 \(L\)은 택시에, \(R\)은 승객에 대응한다고 하겠습니다. 맨 처음에 우리는 \(L\)의 정보만 알고 있습니다. 이후 매 시각마다 \(R\)의 승객이 하나씩 들어옵니다. 동시에 그로부터 각 택시까지의 거리도 알게 됩니다. 그 시각에 바로 우리는 이 승객을 어느 택시에 태울지를 결정해야 합니다. 택시에는 여러 승객이 함께 탑승할 수 없습니다. 어떤 승객을 한 택시에 태운 후에 다른 택시로 갈아 태울 수도 없습니다. 모든 승객은 택시 하나를 할당받아야 합니다. 이때 우리의 목표는 각 승객과 할당된 택시 사이의 거리의 합이 최소가 되도록 하는 것입니다.
매번 가장 가까운 택시에 할당하면 좋지 않은 이유
생각할 수 있는 가장 간단한 방법은 다음과 같겠습니다.
매번 승객이 들어오면 빈 택시 중 그 승객으로부터 가장 가까운 택시에 할당한다.
일견 합리적으로 보이는 이 방법은 사실 매우 멍청한 방법입니다. 다음의 예시를 생각해 봅시다.
- 수직선 상에서 처음 \(n - 1\) 대의 택시를 \(2, 2^2, 2^3, \cdots, 2^{n-1}\)의 위치에 둔다. 마지막 \(n\)번째 택시는 \( -\varepsilon \)의 위치에 둔다.
- 첫 번째 승객은 \(1\)의 위치에서 나타난다. 두 번째 승객부터 마지막 \(n\) 번째 승객까지는 각각 \(2, 2^2, \cdots, 2^{n - 1}\)의 위치에서 나타난다.
수직선 위의 지점들이 삼각 부등식을 이룬다는 점은 잘 알려진 사실입니다. (직접 증명해 보세요!)
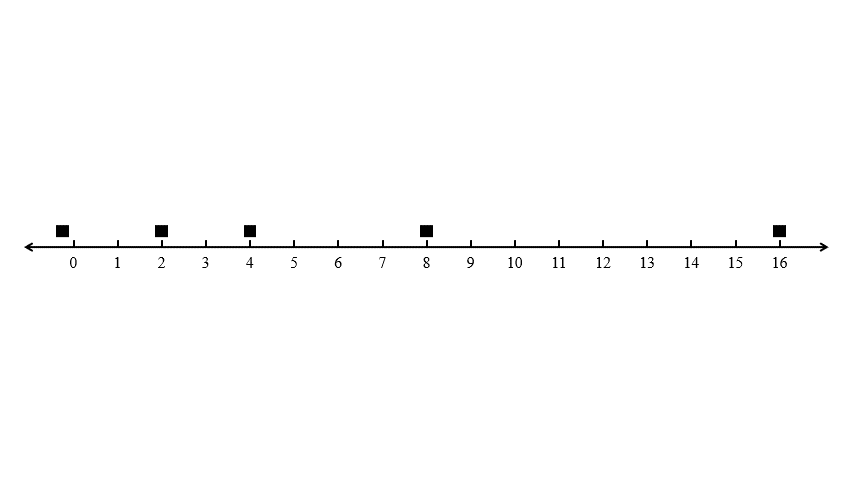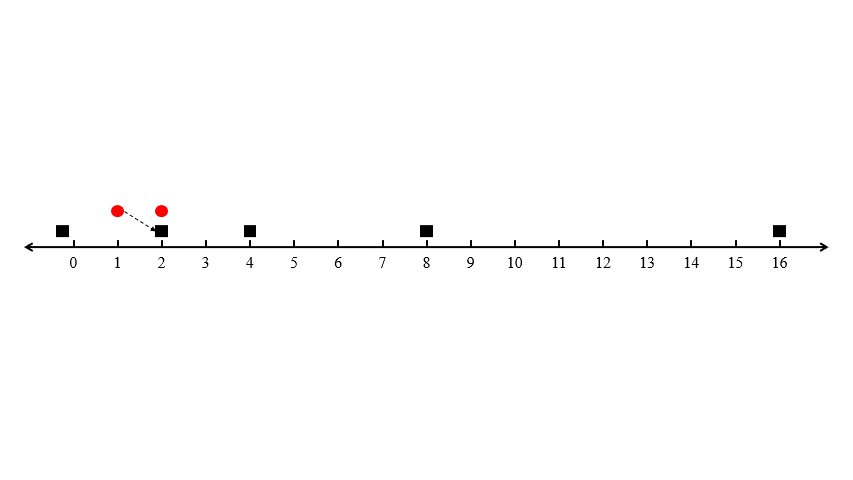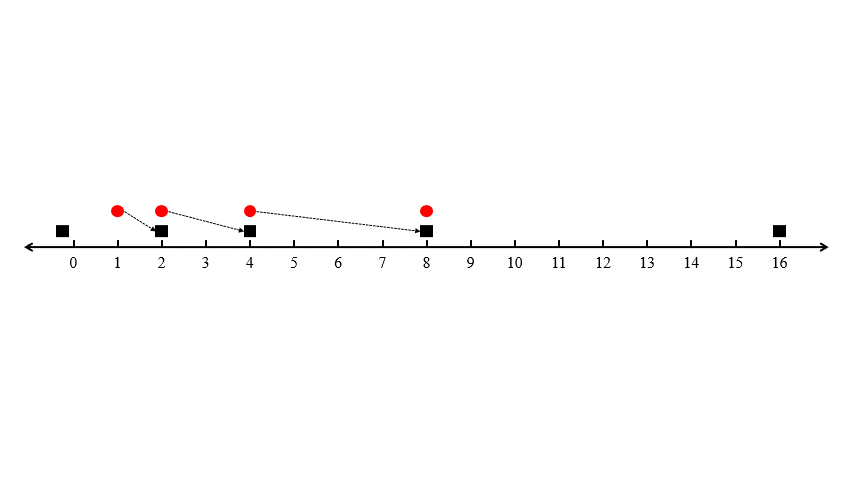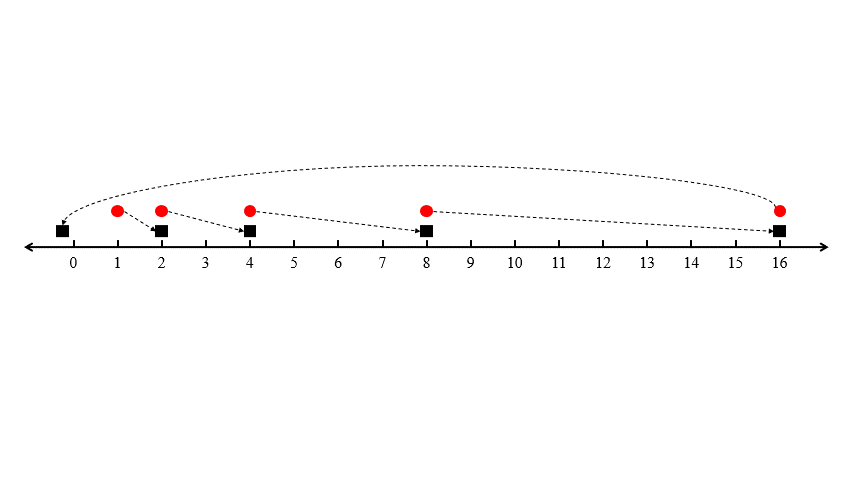
이 입력에서 위 알고리즘이 어떻게 동작하는지를 따져 봅시다. 첫 번째 승객이 들어왔을 때 가장 가까운 택시는 \(2\)의 위치에 있는 첫 번째 택시입니다. 두 번째부터 \(n-1\) 번째의 택시는 자명하게 첫 번째 택시보다 멀리 있으며, 마지막 \(n\)번째 택시는 첫 번째 택시보다 \(\varepsilon\)만큼 멀리 있습니다. 따라서 알고리즘은 첫 번째 승객을 첫 번째 택시에 할당할 것입니다.
이 상태에서 두 번째 택시가 들어왔다고 합시다. 가장 가까운 택시는 같은 위치의 첫 번째 택시입니다만 이는 이미 첫 번째 승객에게 할당된 상태입니다. 가망이 있는 후보는 \(2^2\)의 위치에 있는 두 번째 택시와 \( -\varepsilon \)의 위치에 있는 마지막 택시입니다. 두 번째 승객은 \(2\)의 위치에서 나타나므로, 두 번째 택시까지의 거리는 \( 2^2 - 2 = 2 \)이고 \(n\) 번째 택시까지의 거리는 \( 2 + \varepsilon \)입니다. 따라서 알고리즘은 두 번째 승객을 두 번째 택시에 할당할 것입니다.
같은 이치로 \( i < n \)에 대해, \(i\) 번째 승객이 들어왔을 때, 알고리즘은 이 승객을 \(i\) 번째 택시에 할당하게 됩니다. 왜냐하면 \( i \) 번째 승객과 \(i\) 번째 택시 사이의 거리는 \( 2^i - 2^{i - 1} = 2^{i - 1} \)인 반면 \(n\) 번째 택시까지의 거리는 \( 2^{i - 1} + \varepsilon \)이기 때문입니다.
마지막 승객이 들어오면 남은 택시는 \(-\varepsilon\)의 위치에 있는 \(n\) 번째 택시밖에 없으므로, \( 2^{n - 1} + \varepsilon \)의 거리에 할당해주어야 합니다. 따라서 이 알고리즘이 출력하는 할당의 총 거리는 \[ 1 + 2 + 2^2 + \cdots + 2^{n - 2} + 2^{n - 1} + \varepsilon = 2^n - 1 + \varepsilon \]이 됩니다.
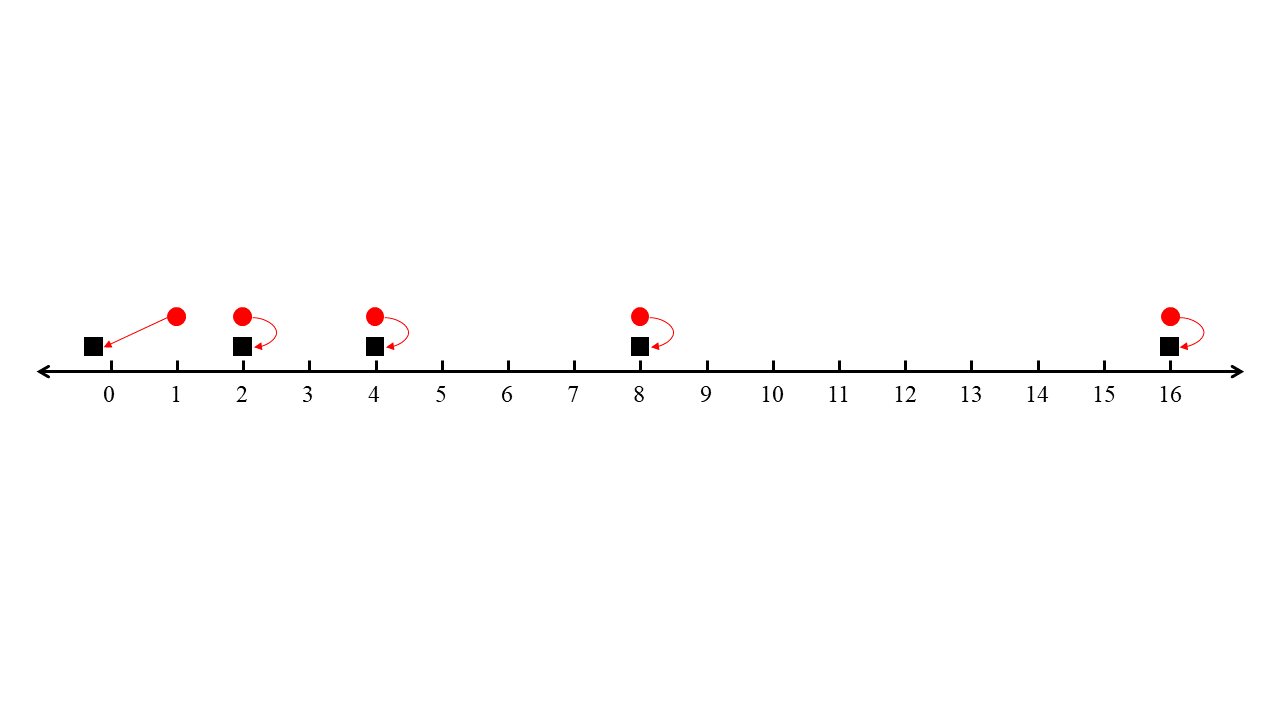
하지만 최적의 할당 방법은 첫 번째 승객을 \(n\) 번째 택시에 할당하고 나머지 승객들을 같은 위치에 있는 택시에 할당시키는 것이죠. 이때의 거리는 \( 1 + \varepsilon \)입니다. 이를 통해 이 알고리즘이 지수적으로 못하는 경쟁비를 갖는다는 사실을 확인할 수 있습니다.
선형 경쟁비 알고리즘
가장 가까운 빈 택시에 할당하는 알고리즘은 안타깝게도 좋은 경쟁비를 가질 수 없었습니다. 어떻게 하면 훨씬 잘할 수 있을까요? 다음 알고리즘을 고려해 봅시다. 아래에서 \(\oplus\)는 대칭차(symmetric difference)를 의미합니다. 즉, 두 집합 \(A, B\)에 대해 \( A \oplus B := (A \setminus B) \cup (B \setminus A) \)입니다.
알고리즘 1. \(2n\)-competitive algorithm for min-distance matching
초기 입력: 택시 정점 집합 \(L\)
출력: 완벽 매칭
- \(M_0 \gets \emptyset, N_0 \gets \emptyset \)
- 매번 \(k\) 번째 승객 \(j_k \in R\)이 들어왔을 때 아래를 수행하자.
- \(R_k\)를 지금까지 들어온 승객의 집합이라고 하자. 즉, \( R_k := \{ j_1, \cdots, j_k \} \)이다. 비슷하게 \(E_k\)를 지금까지 알려진 간선들의 집합이라고 하자.
- \((L \cup R_k, E_k)\)에서 \(R_k\)가 모두 참여하는 최소 거리 매칭을 \(N_k\)라고 하자.
- \( N_{k - 1} \oplus N_k \) 위에서 \(j_k\)를 한 끝으로 하는 증가 경로(augmenting path)의 다른 끝을 \(i_k\)라고 하자.
- \( M_k \gets M_{k - 1} \cup \{ (i_k, j_k) \} \)
- \(M_n\)을 반환한다.
쉽게 말해 이 알고리즘은 매 승객 \(j_k\)를 이번 시각에 최적해 \(N_k\)에서 새로이 할당된 택시 \(i_k\)에 할당하는 방법입니다. 흥미롭게도 이 알고리즘은 이전 알고리즘보다 훨씬 좋은 \(2n\)의 경쟁비를 갖습니다. 이를 증명해 보겠습니다.
먼저 단계 2-b는 헝가리안 알고리즘(Hungarian algorithm)을 사용하면 다항 시간에 해결할 수 있습니다. 궁금하신 분들은 제 이전 포스트를 참고하시기 바랍니다.
2019.08.07 - [조합론적 최적화/Matching] - 할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian Algorithm)
할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian Algorithm)
이번 포스팅에서는 assignment problem과 Hungarian algorithm에 대해서 알아보겠습니다. 먼저 assignment problem이 어떤 것인지에 대해서 살펴보고, 이를 해결하는 방법을 알아보도록 하겠습니다. 인터넷을 찾
gazelle-and-cs.tistory.com
다음으로 단계 2-c에서 \( N_{k - 1} \oplus N_k \)에 \(j_k\)를 한 끝으로 하는 증가 경로가 존재한다는 것도 잘 알려진 사실입니다. 아래 포스트에서 관련한 내용을 자세히 서술하였으니 참고 바랍니다.
2020.02.22 - [조합론적 최적화/Matching] - 호프크로프트-카프 알고리즘 (Hopcroft-Karp Algorithm)
호프크로프트-카프 알고리즘 (Hopcroft-Karp Algorithm)
엄청 오랜만에 포스팅을 합니다. 방학이 되면 시간이 나서 글을 좀 쓸 수 있을 줄 알았는데, 대학원생은 방학도 바쁘군요. 다행히 어느정도 일단락이 나서 이렇게 글을 쓸 수 있게 되었습니다.
gazelle-and-cs.tistory.com
사실, 증명을 위해서는 존재성보다 강력한 아래의 성질이 필요합니다.
정리 1. 대칭차의 구조적 특징
모든 \(k = 1, \cdots, n\)에 대해, \(N_{k - 1} \oplus N_k\)는 정확히 하나의 증가 경로로만 이루어졌다고 가정할 수 있다.
[증명] 먼저 \(R_{k - 1} \subset R_k\)이면서 \(R_k \setminus R_{k - 1} = \{ j_k \}\)임을 확인하시기 바랍니다. \(N_{k - 1}\)와 \(N_k\)는 각각 \( R_{k - 1} \)과 \(R_k\)가 모두 참여하는 매칭이므로 \( N_{k - 1} \oplus N_k \)의 연결 성분(connected component) 중에서 증가 경로는 하나밖에 있을 수 없습니다. 따라서 나머지 성분은 분명 한 택시에서 출발하여 다른 택시에 도달하는 교차 경로(alternating path)나 순환(cycle)이어야 합니다.
이제 일반성을 잃지 않고 교차 경로가 존재하지 않는다고 가정할 수 있음을 보이겠습니다. 어떤 교차 경로가 \[ i_1, j_1, i_2, \cdots, i_\ell, j_\ell, i_{\ell + 1} \]를 순서대로 지난다고 하겠습니다. (이는 기존의 \(j_k\) 정의를 위배하지만, 표현의 편의를 위해 이렇게 정의했습니다.) 이때 일반성을 잃지 않고, 모든 \(p = 1, \cdots, \ell\)에 대해, 각 \( (i_p, j_p) \)는 \(N_{k - 1} \)에 속하고, \( (i_{p + 1}, j_p) \)는 \( N_k \)에 속한다고 합시다.
먼저 이 교차 경로 위에서 각 매칭에 참여하는 간선의 거리의 합은 동일해야 합니다, 다시 말해, \[ \sum_{p = 1}^\ell d(i_p, j_p) = \sum_{p = 1}^\ell d(i_{p+1}, j_p) \tag{1} \]를 만족해야 합니다. 그렇지 않고 만약 한쪽이 다른 쪽보다 작다면, 모순이 발생합니다. 예를 들어 위 식에서 좌변이 크다면 \( N_{k - 1} \) 대신 \[ N_{k - 1} \setminus \{(i_p, j_p) \mid p = 1, \cdots, \ell\} \cup \{ (i_{p+1}, j_p) \mid p = 1, \cdots, \ell \}\]이 더 짧은 거리의 합을 갖는 \(R_{k - 1}\)이 모두 참여하는 매칭이 됩니다. 따라서 \(N_{k - 1}\)이 최소 거리 매칭이라는 사실에 모순을 일으킵니다. 식 1에서 우변이 큰 경우도 비슷하게 \( N_k \)가 최소 거리 매칭이라는 사실에 모순을 유도한다는 점을 알 수 있습니다.
그런데 이때, 식 1이 성립하므로 \(N_k\) 말고 \[ N_k \setminus \{ (i_{p + 1}, j_p) \mid p = 1, \cdots, \ell \} \cup \{ (i_p, j_p) \mid p=1, \cdots, \ell \} \]도 \(R_k\)가 모두 참여하는 최소 거리 매칭이 됩니다.
위와 비슷한 논의로 순환도 제거할 수 있습니다. 위 작업을 모든 교차 경로와 순환에 적용하면 \(N_{k - 1} \oplus N_k\)에 정확히 하나의 증가 경로만 존재한다고 가정할 수 있습니다. ■
매 시각의 최적해 \(N_k\)에서 할당이 된 택시의 집합을 \(L_k\)라고 하겠습니다. 그러면 정리 2를 통해 매번 정확히 하나의 증가 경로만 적용하므로 우리는 \[ L_0 (=\emptyset) \subset L_1 \subset L_2 \subset \cdots \subset L_n (=L) \]이라고 가정할 수 있습니다. 알고리즘의 단계 2-d에서 매번 \( i_k = L_k \setminus L_{k - 1} \)를 \(M_k\)에 새로이 할당시키므로 \(M_k\)에서 할당된 택시의 집합은 정확히 \(L_k\)와 동일합니다. 게다가 \(i_k \not\in L_{k-1} \)이므로 \( M_k \)는 항상 매칭입니다.
이제 출력하는 \(M_n\)의 거리의 합이 그리 크지 않음을 보이겠습니다. \(i_k\)와 \(j_k\)는 \( N_k \oplus N_{k - 1} \)의 증가 경로의 양 끝점이므로, 삼각 부등식에 의해 \[ d(i_k, j_k) \leq d(N_{k -1}) + d(N_k) \]임을 쉽게 알 수 있습니다. 그런데 거리 \(d\)는 음수를 갖지 아니하고 \( N_k \)에서 \(j_k\)를 지워서 얻는 매칭은 \(R_{k - 1}\)이 모두 참여하는 매칭이라는 사실을 통해 \[ d(N_0) \leq d(N_1) \leq d(N_2) \leq \cdots \leq d(N_n) \]이 성립함을 어렵지 않게 보일 수 있습니다. 따라서, \[ d(M_n) = \sum_{k = 1}^n d(i_k, j_k) \leq \sum_{k = 1}^n d(N_{k - 1}) + d(N_k) \leq 2n \cdot d(N_n) \]이 성립합니다. 이로써 알고리즘 1이 2n의 경쟁비를 갖는다는 사실을 증명하였습니다.
점근적으로 선형 경쟁비가 최선인 이유
알고리즘 1은 선형의 경쟁비를 갖습니다. 이는 처음에 고려한 가장 가까운 택시에 할당하는 방법보다는 월등히 좋지만, 여전히 승객의 수가 많을수록 이론적인 성능이 감퇴합니다. 과연 이보다 잘할 수 있을까요? 안타깝게도 결정론적으로는 선형의 경쟁비보다 잘할 수 없음을 보일 수 있습니다. 다시 말해, 알고리즘 1은 점근적으로 최선이라는 뜻이죠.
결정론적 알고리즘의 경쟁비 하한(lower bound)을 구하기 위해서는 특정한 적응형 상대방(adaptive adversary)을 상정하여도 됩니다. 관련하여 자세한 내용은 아래를 참고하세요.
2020.03.14 - [온라인 알고리즘/Basic] - 온라인 알고리즘 (Online Algorithm)
온라인 알고리즘 (Online Algorithm)
일전에 유명한 온라인 문제 중 하나인 online bipartite matching을 다룬 적이 있었습니다. 당시에는 제 지식이 그렇게 깊지 않아서 제대로 설명하지 못했을뿐더러 잘못 전달한 내용도 있었습니다. 최
gazelle-and-cs.tistory.com
다음과 같은 적응형 상대방을 생각해 봅시다. \(n+1\) 개의 지점을 갖고 오겠습니다. 상대방은 이 지점들 위에 택시와 승객을 둘 예정입니다. 같은 지점 사이의 거리는 당연히 0이며, 서로 다른 지점 사이의 거리는 1입니다.
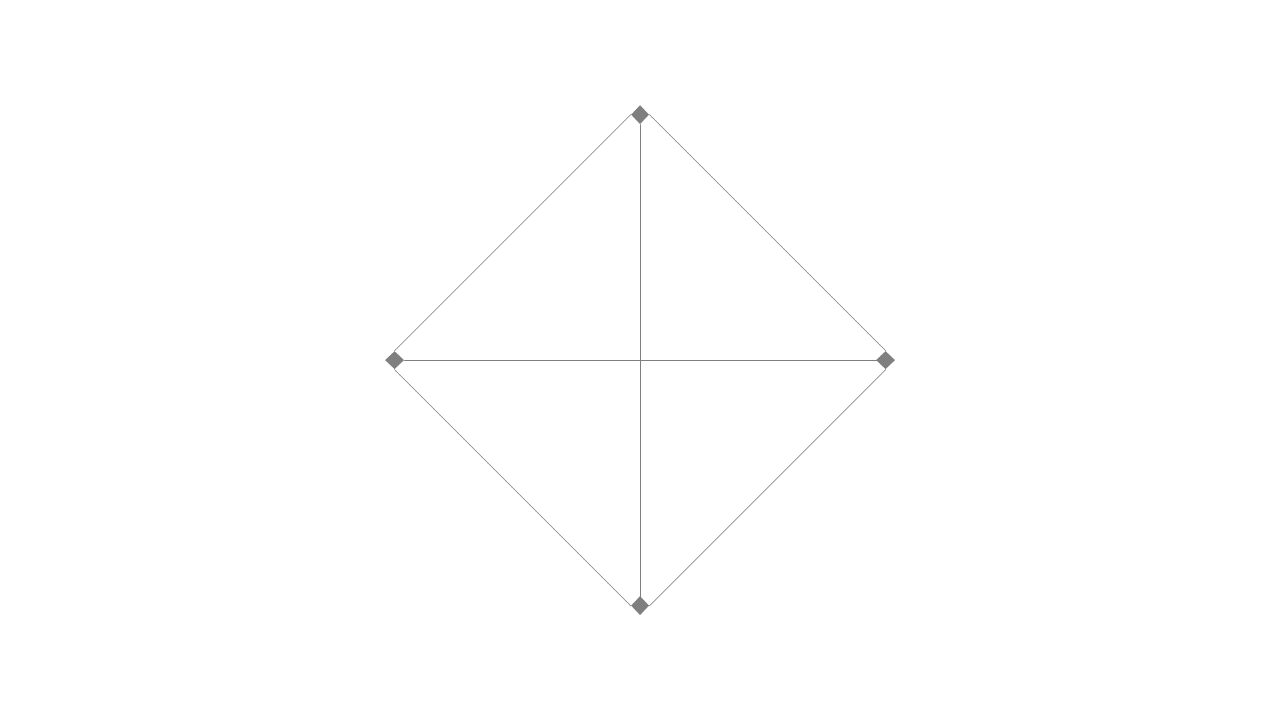
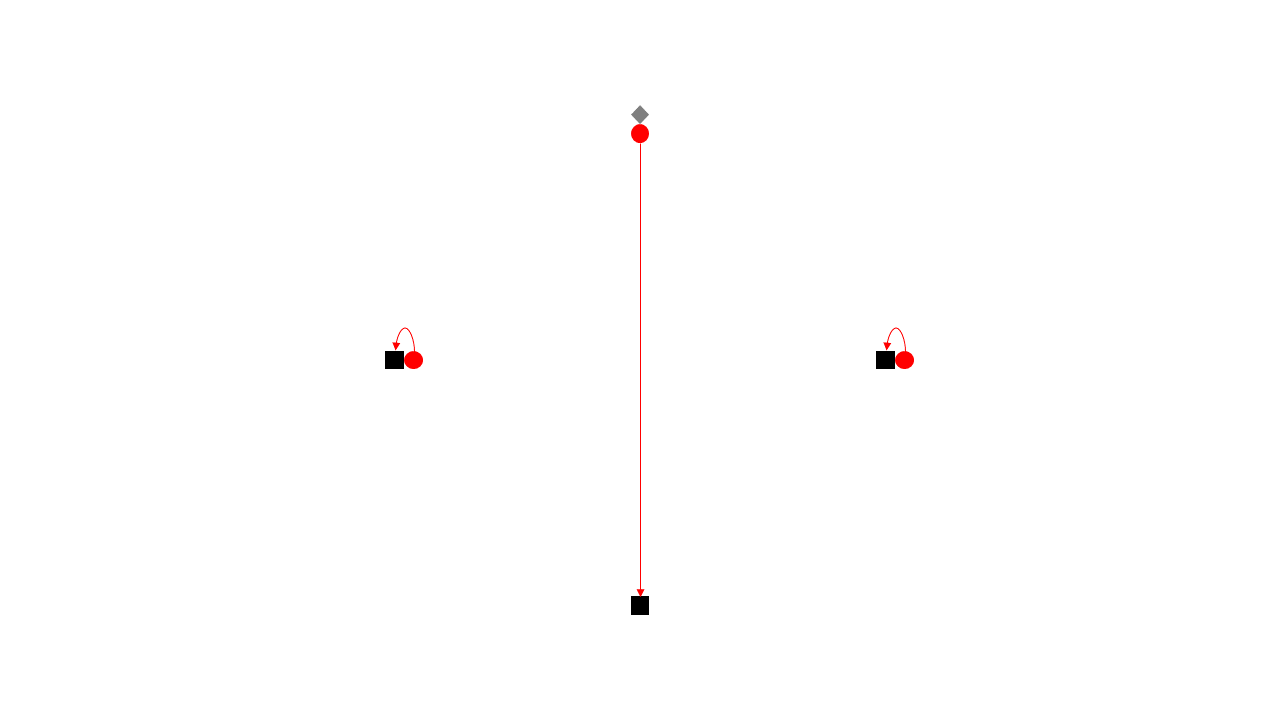
이제 상대방이 어떻게 동작하는지 정의하겠습니다. 택시는 \(n+1\) 개의 지점 중 \(n\) 개의 지점에 둡니다. 첫 번째 승객은 택시가 없는 나머지 한 지점에 나타나게 합니다. 알고리즘은 이 승객을 어느 한 택시에 할당할 것입니다. 상대방은 해당 택시가 위치한 지점에 두 번째 승객을 둡니다. 이 작업을 반복합니다.

어떤 결정론적 알고리즘이든 상대방이 이렇게 동작한다면 매번 거리가 1인 택시에 할당해 주어야 하므로 총 거리는 \(n\)이 됩니다. 하지만 첫 번째 승객을 승객이 나타나지 않는 지점의 택시에 할당해 주고 나머지 승객은 해당 지점의 택시에 할당해 준다면 총 1의 거리로 모든 승객을 태울 수 있습니다. 따라서 \(n\)보다 좋은 경쟁비를 갖는 결정론적 알고리즘은 존재할 수 없습니다.
최대 거리 완벽 매칭
지금까지 최소 거리 완벽 매칭에 대해서 알아 보았습니다. 그렇다면 반대로 거리를 최대화하는 문제는 어떻게 될까요? 사실 거리를 최대화하는 완벽 매칭을 찾을 이유가 딱히 있을지는 모르겠지만, 이 경우에는 최소 거리 완벽 매칭보다 훨씬 좋은 경쟁비로 문제를 해결할 수 있습니다.
참고로 아래 알고리즘은 승객의 수가 택시의 개수보다 크지 않을 때, 즉 \(|R| \leq |L|\)인 경우에는 모두 성립합니다. 사실 그 경우에는 모든 승객을 할당해야 하는 조건이 없어도 괜찮아 보입니다. 하지만, 반대로 \(|R| > |L|\)인 경우에는 좋은 경쟁비를 갖기 어렵습니다. 이전 포스트의 최대 가중치 매칭의 경쟁비 상한(upper bound)을 주는 입력을 그대로 적용할 수 있기 때문입니다.
매번 가장 먼 택시에 할당하는 알고리즘
이전에 최소 거리 완벽 매칭에서는 매번 가능한 택시 중 가장 가까운 택시에 할당하는 알고리즘을 생각해 봤고, 이 알고리즘이 그다지 좋은 경쟁비를 주지 못한다는 사실을 확인했습니다. 최대 거리 완벽 매칭에서도 자연스럽게, 매 승객이 들어올 때마다 가장 먼 택시에 방법을 생각해 봅시다.
놀랍게도 거리가 삼각 부등식을 만족한다면 이 알고리즘은 \(\frac{1}{3}\)의 경쟁비를 갖습니다. 최소 거리 완벽 매칭을 해결하는 선형 경쟁비보다 좋은 결정론적 알고리즘을 만들 수 없는 것에 비해서는 괄목할 만한 성능이 아닐 수 없습니다.
증명을 해보죠. 승객이 모두 들어왔을 때의 최대 거리 매칭 \(N\)을 하나 고정하겠습니다. 여기서 각 승객 \(j \in R\)에 대해 \( N(j) \in L \)를 \(j\)가 탑승한 택시라고 하겠습니다.
이제 알고리즘을 생각해 봅시다. \(k\) 번째 승객 \(j_k\)가 들어왔을 때 알고리즘이 할당한 택시를 \(i_k\)라고 부르겠습니다. 만약 \(N(j_k)\)가 빈 택시였으면, 알고리즘의 동작에 의해 \[ d(N(j_k), i_k) \leq d(i_k, j_k) \]가 만족합니다.
반대로 \( N(j_k) \)가 이미 이전에 들어온 승객 \(j_{k'}\)에 의해 할당이 되었다고 합시다. 즉, \( i_{k'} = N(j_k) \)를 만족합니다. 택시 \(i_k\)는 승객 \(j_k\)가 들어왔을때야 할당이 되므로 승객 \(j_{k'}\)이 들어왔을 때는 빈 택시였습니다. 그러므로 알고리즘의 동작에 의해 \[ d(i_k, j_{k'}) \leq d(i_{k'}, j_{k'}) \]라는 사실을 알 수 있습니다. 그러면 삼각 부등식에 의해, \[ d(N(j_k), j_k) = d(i_{k'}, j_k) \leq d(i_{k'}, j_{k'}) + d(i_k, j_{k'}) + d(i_k, j_k) \leq 2 d(i_{k'}, j_{k'}) + d(i_k, j_k) \]가 성립합니다. (그림 6 참조) 알고리즘은 항상 매칭을 유지하고 한번 짝지어지면 번복이 되지 않으므로 \( j_{k'} \)이 \(j_k\)와는 다른 승객 \(j\)의 \(N(j)\)에 영향을 미치지 않습니다. 다시 말해, \(k \neq \ell\)이면 \( k' \neq \ell' \)을 만족합니다.
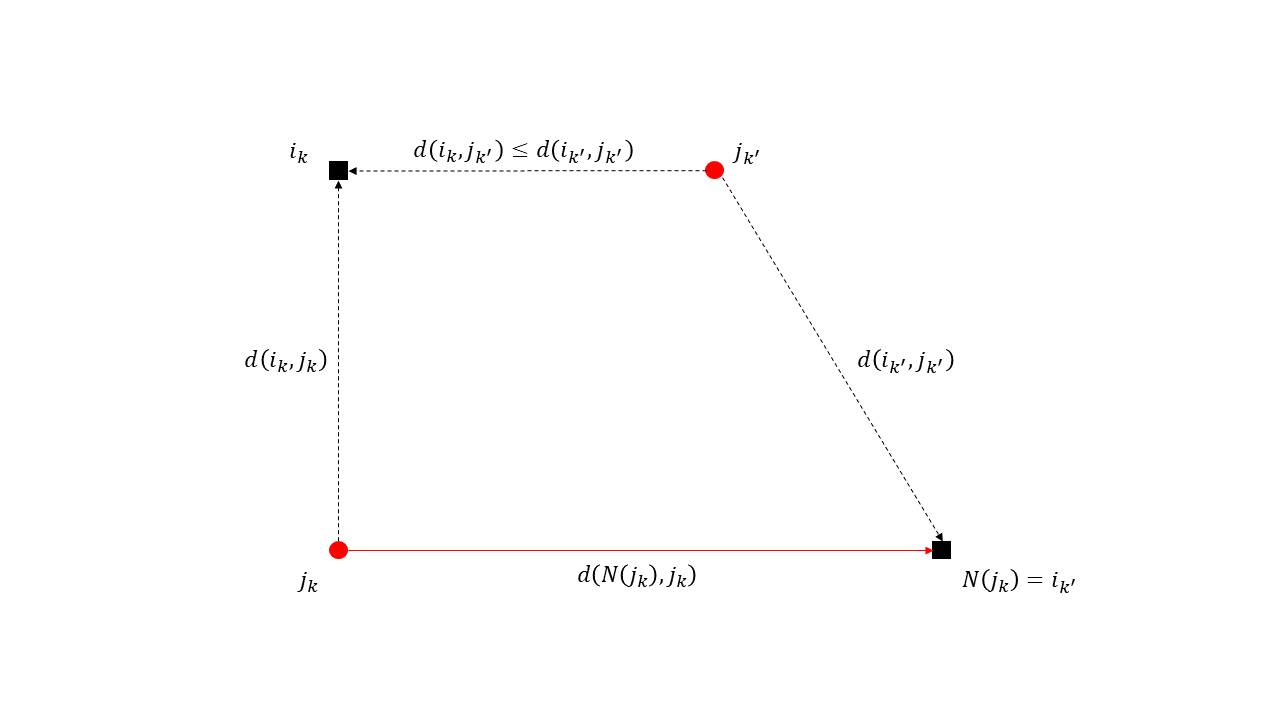
\(R_e\)를 첫 번째 경우에 해당하는 승객의 집합, \(R_m\)을 두 번째 경우에 해당하는 승객의 집합이라고 하겠습니다. 그러면, \[ \begin{array} {rl} d(N) &\displaystyle = \sum_{j_k \in R_e} d(N(i_k), j_k) + \sum_{j_k \in R_m} d(N(i_k), j_k) \\ &\displaystyle \leq \sum_{j_k \in R_e} d(i_k, j_k) + \sum_{j_k \in R_m} \left[ 2 d(i_{k'}, j_{k'}) + d(i_k, j_k) \right] \\ &\displaystyle = \sum_{j_k \in R} d(i_k, j_k) + 2 \sum_{j_k \in R_m} d(i_{k'}, j_{k'}) \\ &\displaystyle \leq 3 \sum_{j_k \in R} d(i_k, j_k) = 3d(M)\end{array} \]를 이끌어낼 수 있습니다. 여기서 마지막 부등식은 각 \(j_k \in R_m\)마다 \(j_{k'}\)이 중복되지 않으므로 \[ \sum_{j_k \in R_m} d(i_{k'}, j_{k'}) \leq \sum_{j_k \in R} d(i_k, j_k) \]가 되기 때문입니다. 이것으로 증명이 끝납니다.
1/3의 경쟁비가 최선인 이유
좋은 경쟁비를 갖는 알고리즘을 만들었으니 남은 질문은 더 잘할 수 있는가입니다. 흥미롭게도 최대 거리 매칭을 결정론적으로 경쟁적으로 해결하는 알고리즘은 \(\frac{1}{3}\)보다 좋은 경쟁비를 가질 수 없습니다.
다음의 상대방을 생각해 봅시다. 먼저 거리를 정의하기 위해서 아래와 같은 가중치가 없는(unweighted) 네트워크를 생각해 보겠습니다. 알고리즘의 입력 \(G=(L \cup R, E)\)와 구분하기 위해 그래프, 정점, 간선이라는 표현 대신 네트워크, 노드, 링크라는 표현을 쓰겠습니다. 먼저 노드는 다음과 같이 구성됩니다.
- \(r\)
- \(x_1, \cdots, x_n\)
- \(y_1, \cdots, y_n\)
링크는 다음과 같이 구성됩니다.
- \((r, x_1), (r, x_2), \cdots, (r, x_n)\) (즉, \(r\)과 모든 \(x_k\) 사이에 링크가 있다.)
- 모든 \(k = 1, \cdots, n\)에 대해, 각 \( (x_k, y_1), \cdots, (x_k, y_{k - 1}), (x_k, y_{k + 1}), \cdots, (x_k, y_n) \) (다시 말해서, 모든 쌍 중에서 각 \((x_k, y_k)\)를 뺀 나머지 쌍 사이에 링크가 있다.)
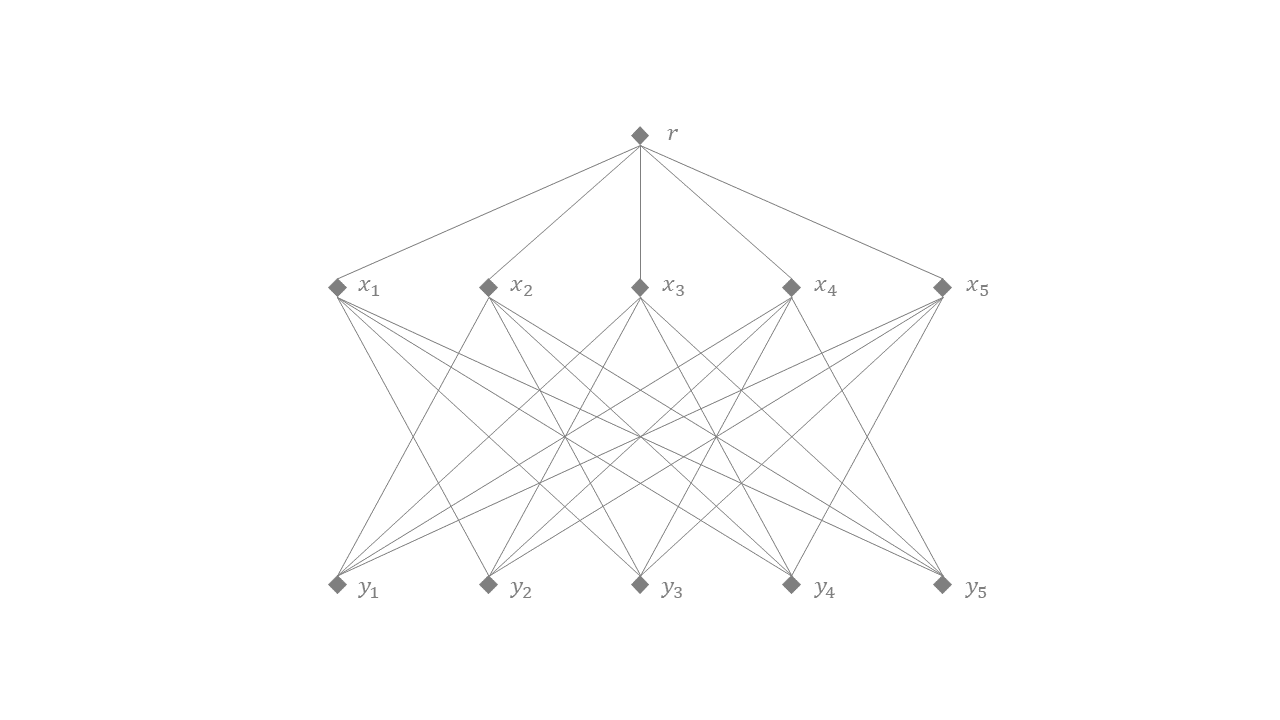
이제 두 지점 사이의 거리 \(d\)를 정의하겠습니다. 가능한 지점은 위 네트워크의 노드와 같습니다. 임의의 두 지점 \(u, v\) 사이의 거리는 노드 \(u\)에서 노드 \(v\)까지의 최단 경로의 길이로 하겠습니다. 예를 들어, 아래 증명에서 사용할 거리를 적어 보자면, 임의의 \(k, \ell\)에 대해, \[ d(r, x_k) = 1, \quad d(x_k, y_\ell) = \left\{ \begin{array}{ll} 3, & k = \ell, \\ 1, & k \neq \ell \end{array} \right. \]이 됩니다. 이렇게 정의된 거리가 삼각 부등식을 만족한다는 사실은 잘 알려져 있습니다. (왜 그럴까요? 이것도 직접 증명해 보세요!)
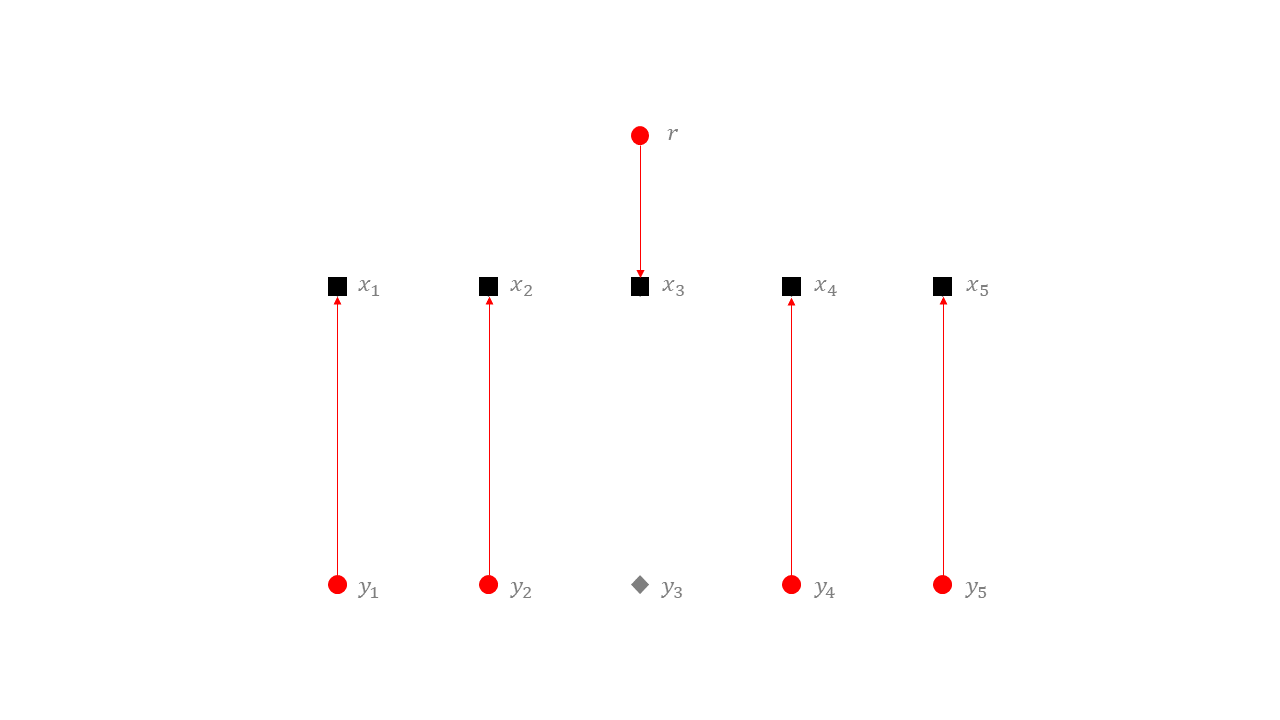
이제 상대방의 동작을 정의하겠습니다. 먼저 택시는 \(x_1, \cdots, x_n\)의 지점에 각각 둡니다. 첫 번째 승객은 \(r\)에 둡니다. 만약 알고리즘이 이 그러면 알고리즘은 이 승객을 어떤 택시에 할당할 것입니다. 그 택시가 \(x_k\)의 위치에 있었다고 합시다. 그러면 상대방은 두 번째 승객을 \( y_k \)의 위치에 나오도록 합니다. 첫 번째 승객이 이미 \(x_k\)에 있는 택시를 잡고 있으므로 알고리즘은 이 승객을 또 다른 위치 \(x_{k'} \)의 택시에 할당할 것입니다. 이번에 상대방은 다음 승객을 \(y_{k'}\)의 위치에 나오도록 만듭니다. 이런 방식을 계속 반복합니다.

상대방에 의해 어떤 결정론적 알고리즘이라도 매 승객을 1만큼 떨어진 거리의 택시에 할당할 수 밖에 없습니다. 따라서 최종 거리의 합은 \(n\)이 됩니다. 하지만 \(y_k\)에 생성된 승객을 \(x_k\)의 택시에 할당하고, 승객이 생성되지 않은 지점에 대응하는 택시에 \(r\)에 생성된 첫 번째 승객을 할당한다면 거리의 합은 정확히 \( 3 (n - 1) + 1 = 3n - 2 \)이 됩니다. 따라서 어떤 결정론적 알고리즘도 \( \frac{n}{3n - 2} \to \frac{1}{3} \)보다 좋은 경쟁비를 얻을 수 없습니다.
마치며
이것으로 가중치가 삼각 부등식을 만족하는 온라인 가중치 이분 매칭에 대한 설명을 모두 마칩니다. 최소 거리 완벽 매칭에 대해서는 \(2n\)의 경쟁비를 갖는 알고리즘이 존재하며, 이는 결정론적으로 (점근적으로) 최선의 방법입니다. 최대 거리 완벽 매칭에 대해서는 \(\frac{1}{3}\)의 경쟁비를 갖는 단순한 알고리즘이 존재하며, 이것도 결정론적으로는 최선의 방법입니다.
이번 글을 적은 이유는 최소 거리 완벽 매칭 때문입니다. 처음에 저는 매번 가장 가까운 택시에 할당하는 것이 최선의 알고리즘이라고 생각했었습니다. 그런데 혼자 증명을 시도하는 중에 그 알고리즘이 \( \Omega \left( \frac{2^n}{n} \right) \)보다 좋은 경쟁비를 가질 수 없다는 것을 알게 되었습니다. 부랴부랴 논문을 뒤져서 제가 잘못 생각하고 있었다는 것을 알게 되었습니다. 다시 공부한 겸사로 작성한 것이 이번 글입니다.
이번 글에서는 랜덤 알고리즘에 대한 내용은 다루지 않았습니다. 최소 거리 완벽 매칭에 대해서는 관련하여 다양한 결과가 있는 것으로 알고 있습니다만, 제가 아직 그쪽까지는 제대로 공부하지 않았습니다. 나중에 공부하게 되면 포스팅해 보도록 하겠습니다. 반면 최대 거리 완벽 매칭은 아무래도 풀어야 할 정당성이 부족한 문제이다 보니 연구가 덜 되었습니다. 하지만 개인적으로는 랜덤성이 최대 거리 이분 매칭에 어떻게 영향을 줄 수 있을지 궁금하기도 합니다.
읽어 주셔서 고맙습니다 :)
참조
[1] Bala Kalyanasundaram and Kirk Pruhs. "Online weighted matching." Journal of Algorithms 14, no. 3 (1993): 478-488.
[2] Samir Khuller, Stephen G. Mitchell, and Vijay V. Vazirani. "On-line algorithms for weighted bipartite matching and stable marriages." Theoretical Computer Science 127, no. 2 (1994): 255-267.
'온라인 알고리즘 > Online matching' 카테고리의 다른 글
| 온라인 이분 매칭 경쟁비 상한 (Upper Bound of Competitive Ratio for Online Bipartite Matching) (2) | 2024.03.12 |
|---|---|
| 온라인 분수 이분 매칭 (Online Fractional Bipartite Matching) (3) | 2024.02.03 |
| 온라인 가중치 이분 매칭 (Online Weighted Bipartite Matching) (0) | 2021.02.14 |
| 온라인 이분 매칭 랭킹 알고리즘 (Ranking Algorithm for Online Bipartite Matching) (0) | 2021.01.09 |
| 온라인 이분 매칭 (Online Bipartite Matching) (0) | 2020.11.07 |



