이번 포스팅에서는 assignment problem과 Hungarian algorithm에 대해서 알아보겠습니다. 먼저 assignment problem이 어떤 것인지에 대해서 살펴보고, 이를 해결하는 방법을 알아보도록 하겠습니다. 인터넷을 찾아보니 Hungarian algorithm 자체가 어떻게 동작하는지에 대해서는 우리말로 된 포스팅이 많이 있는 반면에 이 알고리즘이 왜 정확히 돌아가는지에 대해서 분석한 글은 보지 못하였습니다. 제 블로그는 이 간격을 열심히 줄이는 데 초점이 맞추어져 있습니다. 그러니 이번에도 왜 이 알고리즘이 올바른 결과를 출력하는지 함께 알아보도록 하죠.
문제 정의

문제를 정의하기 전에 제 하소연부터 좀 하겠습니다. 이 글을 작성하는 현재 제 자취방 에어컨이 고장 난 상태입니다. 에어컨 수리 기사님은 실외기가 고장났다고 하셨습니다. 문제는 실외기가 창문이 나지 않은 외벽에 붙어있어서 접근이 불가능하다는 점입니다. 어쩔 수 없이 중장비를 부르겠다고 하시고는 그냥 가셨습니다. 다행히 장마로 비가 추적추적 내려 그렇게 덥지는 않습니다. 그렇지만 습도는 어찌할 방도가 없네요.
이번 주제는 assignment problem인데 갑자기 제가 왜 이런 신변잡기를 주저리 늘어놓고 있는지 궁금하실 것입니다. 바로 이 문제를 어떻게 설명하면 좋을까 고민하다가 오늘 아침에 일어난 일이 좋은 예시가 될 것 같아서 가지고 왔습니다. (아, 물론 습한 상태를 약간 한탄하는 것도 있기는 합니다만, 현재로서는 에어컨이 빨리 고쳐지기를 바랄 뿐입니다.) 바로 수리 기사님을 할당하는 방법에 관한 것입니다. 분명히 저와 같이 에어컨에 문제가 생긴 사람들이 방문 수리를 신청했을 것입니다. 그리고 전국에는 서비스 센터가 있지요. 하지만 집집마다 서비스 센터가 바로 옆에 붙어있지는 않을 겁니다. 그렇다면 분명히 어느 서비스 센터의 수리 기사를 어디에 방문하도록 할당을 해 주어야 합니다.
이를 좀 더 엄밀하게 정의해 보겠습니다. 먼저, 방문 수리 신청과 같이 처리해야 할 작업이 주어지겠죠. 그리고 수리 기사님처럼 작업을 수행할 노동자가 있을 것입니다. 마지막으로 어떤 노동자가 어떤 작업을 처리할 때 들어가는 비용을 알아야 합니다. 우리의 목표는 분명 주어진 모든 작업에 노동자를 한 명씩을 가장 적은 비용으로 할당하는 것이 되겠죠.
수학적인 기호와 정의를 사용하면 문제를 좀 더 압축적으로 표현할 수 있습니다. 노동자의 집합을 \(I\), 작업의 집합을 \(J\)라고 하겠습니다. 어떤 노동자 \(i \in I\)가 작업 \(j \in J\)를 처리할 때 들어가는 비용을 \(c(i, j)\)라고 하겠습니다. 문제를 간단하게 만들기 위해서 \(|I| = |J|\)라고 가정하겠습니다. 우리의 목표는 \(I\)에서 \(J\)로 가는 일대일 대응(bijection) \(\sigma : I \rightarrow J\) 중에서 가장 비용이 적은 것을 찾는 것입니다. 다시 말해서,
\[\sum_{i \in I} c(i, \sigma (i))\]
를 최소화시키는 \(\sigma\)를 구하는 것이죠.
우리는 이 문제를 그래프 위에서 생각할 수 있습니다. 노동자 집합 \(I\)를 왼쪽에 나열하고 작업 집합 \(J\)를 오른쪽에 나열합니다. 그후, 노동자 \(i\)와 작업 \(j\)를 잇는 간선을 만들고 그것의 비용을 \(c(i, j)\)로 설정합니다. 그러면 \(I\)와 \(J\)로 양분되고 edge cost가 \(c\)인 complete bipartite graph를 얻게 됩니다. 이 그래프에서 무엇을 찾아야 할까요? 모든 노동자는 한 개의 작업을 할당받아야 하며, 모든 작업은 정확히 한 명의 노동자로부터 처리되어야 합니다. 그래프에서 이러한 성질을 만족하는 것이 무엇인지 우리는 잘 알고 있죠. 바로, matching입니다. 그 중에서도 모든 정점이 참여를 해야 하므로 perfect matching을 찾는 것이겠죠. 게다가 비용을 최소화시켜야 하므로,
\[ \sum_{(i, j) \in M} c(i, j)\]
가 가장 작은 perfect matching \(M\)을 찾는 것이 목표가 되겠습니다.
직관적으로 이해하기
문제가 무엇인지 알았으니 이제부터 알고리즘을 알아보도록 하죠. 먼저 예시를 통해서 알고리즘이 어떻게 돌아가는지 간단히 살펴보도록 하겠습니다. 문제의 입력이 다음과 같이 주어졌다고 생각해 보겠습니다. 아래의 행렬에서 노동자는 행에 대응하며 작업은 열에 대응합니다.
| \(j_1\) | \(j_2\) | \(j_3\) | |
| \(i_1\) | 3 | 8 | 9 |
| \(i_2\) | 4 | 12 | 7 |
| \(i_3\) | 4 | 8 | 5 |
예를 들어, 노동자 \(i_1\)이 작업 \(j_1\)을 할당받으면 3의 비용이 발생합니다. 만약 노동자 \(i_2\)가 작업 \(j_3\)를 할당받으면 7의 비용이 발생하게 되겠죠.
이제부터 solution을 찾아보도록 하죠. 먼저 노동자 \(i_1\)을 살펴보겠습니다. 첫 번째 작업을 할당받으면 3, 두 번째 작업은 8, 마지막 작업은 9의 비용이 발생합니다. 여기서 우리는 어찌되었든 비용이 3만큼은 발생한다는 것을 알 수 있습니다. 따라서 각각의 비용에 3을 모두 빼줘도 (값에는 변화가 있을지라도) solution 자체에는 변화가 없을 겁니다. 즉 이런 식으로 행렬을 만들어도 문제가 없다는 것입니다.
| \(j_1\) | \(j_2\) | \(j_3\) | ||
| \(i_1\) | 0 | 5 | 6 | 3 |
| \(i_2\) | 4 | 12 | 7 | |
| \(i_3\) | 4 | 8 | 5 |
이 작업을 꼭 \(i_1\)에 대해서만 해줄 필요는 없겠죠. 모든 노동자들에게 똑같이 해주면 다음과 같은 행렬을 얻게 됩니다.
| \(j_1\) | \(j_2\) | \(j_3\) | ||
| \(i_1\) | 0 | 5 | 6 | 3 |
| \(i_2\) | 0 | 8 | 3 | 4 |
| \(i_3\) | 0 | 4 | 1 | 4 |
게다가 이 작업을 굳이 노동자에게만 적용할 필요도 없습니다. 모든 작업에 대해서도 비슷한 방식으로 생각할 수 있습니다.
| \(j_1\) | \(j_2\) | \(j_3\) | ||
| \(i_1\) | 0 | 1 | 5 | 3 |
| \(i_2\) | 0 | 4 | 2 | 4 |
| \(i_3\) | 0 | 0 | 0 | 4 |
| 0 | 4 | 1 |
이렇게 얻은 행렬은 한 가지 중요한 성질이 있습니다. 바로, 모든 원소의 값이 0보다 크거나 같다는 것이죠. (심지어 이는 원래 행렬에 음수가 있을 때에도 성립합니다.) 따라서, 0의 값을 가지는 노동자-작업 쌍만 가지고 모든 노동자를 서로 다른 작업에 할당한다면, 이는 가장 적은 비용을 발생할 것입니다.
하지만, 위 행렬에서는 그렇게 할당할 수 없습니다. 왜 그럴까요? 그 이유는 지난 포스팅에서 얻을 수 있습니다. 바로 Kőnig's theorem입니다.
Kőnig's theorem
모든 bipartite graph에서 maximum-size matching의 크기는 minimum-size vertex cover의 크기와 같다.
혹시 이 정리에 대해서 잘 모르신다면 이전 포스팅을 참조해 주세요.
2019/01/28 - [조합론적 최적화/Bipartite matching] - 쾨니그의 정리 (Kőnig's Theorem)
쾨니그의 정리 (Kőnig's Theorem)
이 글은 홀의 정리 (Hall's Theorem) 밀접한 연관이 있습니다. 필요한 경우에는 이를 참조하세요. 2019/01/28 - [조합론적 최적화] - 홀의 정리 (Hall's Theorem) 무언가를 최적화시키는 문제를 보면 생각보다 많..
gazelle-and-cs.tistory.com
이 정리가 왜 0의 값을 가지는 노동자-작업 쌍만으로 할당하는 방법이 없는지를 의미하는지 알아봅시다. 이는 문제를 정의할 때 말씀드린 그래프 관점에서 생각하는 것이 좋습니다. 우리는 0의 값을 가지는 쌍으로만 할당을 하고 싶으니, 해당하는 노동자-작업 간선만 가지는 bipartite graph를 고려하면 됩니다. 즉, 다음과 같은 그래프가 되겠죠.
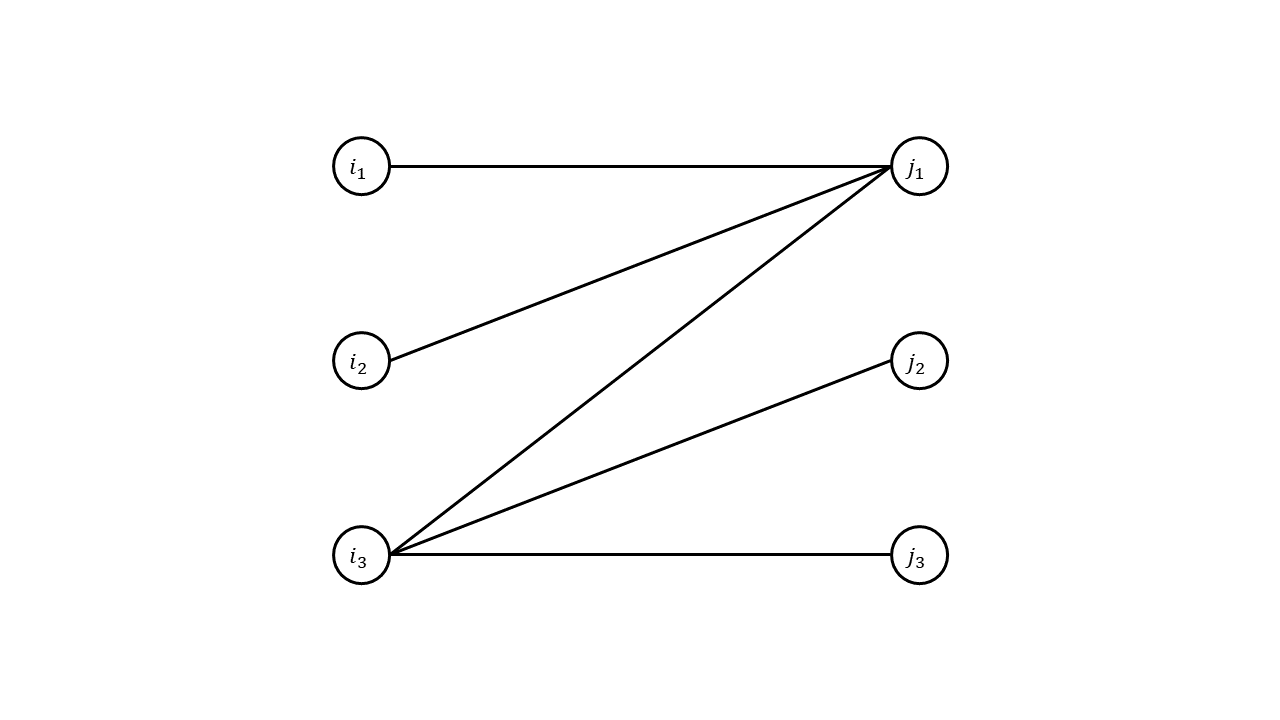
Kőnig's theorem에 의해서 이 그래프에서 maximum-size matching은 minimum-size vertex cover와 동일합니다. 근데 위 그래프에서 우리는 크기가 2인 vertex cover를 발견할 수 있습니다.

따라서 이 그래프에서는 perfect matching이 존재하지 않으며, 자연스럽게 이 행렬에서는 0으로만 이루어진 쌍으로 할당하는 방법은 존재하지 않는다는 것도 알 수 있게 됩니다.
여기서 알고리즘을 끝낼 수는 없습니다. 분명히 optimal solution은 존재할 테니까요. 무언가 조치를 취해야 할텐데 과연 무엇을 할 수 있을까요? 앞에서 우리가 우리 마음대로 설정한 것이 있습니다. 바로 각 노동자(행)와 각 작업(열)에 일정 값을 동일하게 빼 주었습니다. 이 값들을 우리가 잘 조정하여, 행렬의 모든 원소가 0 이상이고 0으로만 이루어진 노동자-작업 쌍으로 모든 노동자를 서로 다른 작업에 할당하는 방법이 있도록 만들어준다면 알고리즘은 성공할 것입니다.
그러기 위해서는 앞에서 구한 minimum-size vertex cover를 가지고 와야 합니다. 이는 노동자 \(i_3\)와 작업 \(j_1\)이었습니다.
| \(j_1\) | \(j_2\) | \(j_3\) | ||
| \(i_1\) | 0 | 1 | 5 | 3 |
| \(i_2\) | 0 | 4 | 2 | 4 |
| \(i_3\) | 0 | 0 | 0 | 4 |
| 0 | 4 | 1 |
이 행렬을 변화시키려면 \(i_3\)와 \(j_1\)으로는 덮어지지 않는 값에 무언가 작업을 해주어야 합니다. 그중 가장 작은 값은 1이므로, 이를 덮어지지 않는 행에 다음과 같이 빼주도록 합시다.
| \(j_1\) | \(j_2\) | \(j_3\) | ||
| \(i_1\) | -1 | 0 | 4 | 3 + 1 |
| \(i_2\) | -1 | 3 | 1 | 4 + 1 |
| \(i_3\) | 0 | 0 | 0 | 4 |
| 0 | 4 | 1 |
이러면 분명히 새로운 0이 하나 생길 것입니다. 하지만 여기서 또 문제는 음수가 생겼다는 점입니다. 우리는 모든 행렬의 원소들을 음이 아닌 수로 만들고자 했으므로 이를 수정해 주어야 합니다. 방법은 간단합니다. 분명 음수가 된 원소는 \(j_1\)에 의해서 cover가 되었을 것입니다. 그러니 이번에는 \(j_1\)에다가 1을 더해주면 되는 것이죠.
| \(j_1\) | \(j_2\) | \(j_3\) | ||
| \(i_1\) | 0 | 0 | 4 | 3 + 1 |
| \(i_2\) | 0 | 3 | 1 | 4 + 1 |
| \(i_3\) | 1 | 0 | 0 | 4 |
| -1 | 4 | 1 |
지금까지 제가 표의 가장자리에 있는 값들을 각 행과 열에 맞게 빼주었기 때문에 \(j_1\)에 더해주는 것은 -1로 표현하였습니다. 자, 이렇게 얻은 행렬에는 우리가 원하는 할당이 존재할까요? 그렇습니다. 바로 다음과 같이 말이죠.
| \(j_1\) | \(j_2\) | \(j_3\) | ||
| \(i_1\) | 0 | 0 | 4 | 4 |
| \(i_2\) | 0 | 3 | 1 | 5 |
| \(i_3\) | 1 | 0 | 0 | 4 |
| -1 | 4 | 1 |
이는 원래 입력에서 다음과 같습니다.
| \(j_1\) | \(j_2\) | \(j_3\) | |
| \(i_1\) | 3 | 8 | 9 |
| \(i_2\) | 4 | 12 | 7 |
| \(i_3\) | 4 | 8 | 5 |
알고리즘
앞에서 설명한 내용을 토대로 알고리즘을 기술하면 다음과 같습니다.
Hungarian algorithm
입력: 노동자 \(I\), 작업 \(J\) (단, \(|I|=|J|=n\)), 비용 \(c : I \times J \rightarrow \mathbb{Q} \)
출력: 가장 적은 비용으로 모든 노동자를 서로 다른 작업에 할당
- 입력을 행은 \(I\), 열은 \(J\), 각 \(i\) 행 \(j\) 열 원소는 \(c(i,j)\)로 이루어진 행렬을 생각한다.
- 모든 행에 대해서, 그 행의 각 원소에 그 행에서 가장 작은 값을 뺀다.
- 모든 열에 대해서, 그 열의 각 원소에 그 열에서 가장 작은 값을 뺀다.
- 행과 열을 합해서 \(n\) 개보다 적게 뽑아 행렬의 모든 0의 값을 갖는 원소를 덮는 방법이 없을 때까지 아래를 반복한다.
- 그러한 방법 중 가장 크기가 작은 것을 \(I^\prime \subset I\), \(J^\prime \subset J\)라고 하자. 즉, \(|I^\prime| + |J^\prime|\)이 가장 작은 것을 가지고 온다.
- \(I^\prime\)과 \(J^\prime\)에 의해서 덮어지지 않는 원소 중 가장 작은 값을 \(\epsilon\)이라고 하자.
- \(I^\prime\)에 속하지 않은 행에 대해서, 그 행의 각 원소를 \(\epsilon\)만큼 뺀다.
- \(J^\prime\)에 속하는 열에 대해서, 그 열의 각 원소를 \(\epsilon\)만큼 더한다.
- 행렬에서 0의 값을 갖는 원소로만 모든 노동자를 서로 다른 작업에 할당한다.
이 알고리즘이 바로 Hungarian algorithm입니다. 이 알고리즘은 1955년 H. W. Kuhn에 의해서 발표가 되었습니다. 한 가지 재미있는 점은 Kuhn이 헝가리 사람이 아닌 미국 사람이라는 점입니다. 그가 이름을 그렇게 붙인 이유는 그의 알고리즘이 두 헝가리 수학자 D. Kőnig과 J. Egerváry의 성과를 토대로 만들었기 때문입니다.
이 알고리즘이 다항 시간에 동작한다는 것은 조금 나중인 1957년 J. Munkres에 의해서 밝혀졌습니다. 하지만 이번 글에서는 이 알고리즘이 다항 시간에 동작한다는 것은 따로 보이지 않으려고 합니다. 그것까지 모두 담기에는 글이 너무 길어질 것 같아서요.
분석
그럼 이제 알고리즘이 제대로 동작한다는 것을 분석해 봅시다. 사실, 직관적으로 이해하기 절에서 중요한 내용은 모두 설명하였습니다. 이를 하나씩 짚어본다는 느낌으로 설명해 보겠습니다.
첫 번째는 바로 입력으로 주어지는 행렬의 행과 열에 같은 수를 더하거나 빼도 결과에는 영향을 미치지 않는다는 것입니다. 증명은 매우 간단합니다. 만약에 우리가 어떤 행의 각 원소에 \(k\) 씩 더했다고 가정해 봅시다. 우리가 찾고자 하는 것은 모든 노동자들이 정확히 하나의 작업을 가지는 방법을 구하는 것입니다. 즉, 어떤 할당 방법을 가지고 오더라도 현재 고려하는 노동자(행)는 정확히 하나의 작업(열)을 할당받을 것이므로 비용은 정확히 \(k\)가 증가하게 됩니다. 열에 대해서 고려하거나, 어떤 값을 뺀다고 하더라도 이는 계속 유효합니다.
따라서 알고리즘의 2번과 3번 단계를 거쳐도 optimal solution은 그대로라는 사실을 알 수 있죠. 게다가 그 단계를 거치면 행렬의 모든 원소가 0보다 크거나 같은 값을 가진다는 것도 알 수 있습니다. 이 성질은 매우 중요합니다. 왜냐면, 만약 우리가 0의 값을 갖는 원소만을 가지고 노동자에게 작업을 할당시켜줄 수 있다면, 이는 곧 optimal solution이 되기 때문이죠. 모든 원소가 0보다 크거나 같다면 0의 비용을 갖는 방법이 가장 좋은 것 아니겠어요?
안타깝지만, 3번 단계가 끝난 직후에 그런 할당이 존재하지 않을 수도 있습니다. 당장에 위의 예시에서도 그러했으니 말이죠. 그렇다면 존재하는지, 아니면 하지 않는지를 어떻게 판단할 수 있을까요? 네, 바로 Kőnig's theorem 덕분이었습니다. 0의 비용을 갖는 노동자와 작업 쌍만 간선으로 연결한 bipartite graph를 생각해 볼 때, 거기서의 matching의 최대 크기는 vertex cover의 최소 크기와 같습니다. 그래프에서의 vertex cover는 행렬에서 행과 열을 선택하는 것에 대응합니다. 즉, 행과 열을 잘 선택해서 모든 0을 덮는 방법을 찾는 것이죠. 이는 알고리즘의 4번 단계에서 기술되어 있습니다.
4번 단계의 내부에서는 각 행과 열마다 빼준 값을 잘 조절하는 작업이 진행됩니다. 일단 이 단계에서의 작업을 모두 거친 후에도 행렬의 모든 원소가 0보다 크거나 같은지를 보여야 합니다. 조절하기 전에 주어지는 행렬의 모든 원소가 0보다 크거나 같다는 것은 가정해도 괜찮습니다. (흔한 수학적 귀납법이죠.) 알고리즘의 4-iii 단계에서 \(I^\prime\)에 속하지 않은 행에 대해서 \(\epsilon\)을 빼줍니다. 그러고 난 후, 만약 \(c(i,j) < 0\)이라면, 이는 \(j \in J^\prime\)을 의미합니다. 그렇지 않다면 4-ii 단계에 어긋나게 되니까 말이죠. 즉, \(c(i,j) = -\epsilon\)이 되며, 4-iv 단계에서는 다시 0으로 바뀌게 됩니다.
우리가 마지막으로 보일 것은 이 알고리즘이 과연 끝이 날 것인가 입니다. 무슨 말이냐면, 만약에 4번 단계에서 조절해 주는 작업이 전혀 도움이 되지 않아 계속 4번 단계에 머물게 될 수도 있지 않겠냐는 것입니다. 일단 확실한 것은
\[\epsilon > 0 \tag{1} \]
이라는 점입니다. 그렇지 않으면 \(I^\prime\)이나 \(J^\prime\)에 의해서 덮혀졌어야 합니다. 이를 어떻게 잘 써먹어 볼 수 있을까요?
만약 어떤 원소가 한번 0이 된 후에는 계속 0으로 남아있다면 아무래도 증명하기 쉬워 보입니다. 하지만 안타깝게도 그렇지 않습니다. 만약 \(i \in I^\prime\), \(j \in J^\prime\)인 경우에는 4-iii에서는 \(\epsilon\)이 빠지지 않지만 4-iv에서는 \(\epsilon\)이 더해져서 0이 되지 않습니다.
위 명제는 성립하지 않지만 다행히 다른 방식으로 증명할 수는 있습니다. 바로 4번 단계를 한 번씩 거칠 때마다 행렬의 모든 원소의 합이 유의미한 크기로 줄어든다는 성질 때문입니다. 4-iii 단계에서 우리는 \(I^\prime\)에 속하지 않은 행 위의 모든 원소마다 \(\epsilon\)을 빼주었습니다. 따라서 총
\[\epsilon \cdot (n - |I^\prime|) \cdot n \]
만큼 감소하게 됩니다. 반대로 4-ii 단계에서는 \(J^\prime\)에 속한 열의 각 원소마다 같은 값을 더해주었지요. 즉,
\[\epsilon \cdot n \cdot |J^\prime| \]
만큼 증가하게 되는 것이죠. 위의 두 식을 통해서, 4번 단계가 한 번 끝날 때마다 행렬의 모든 원소의 합이 정확히
\[\epsilon \cdot n \cdot (n - |I^\prime| - |J^\prime|) \tag{2} \]
만큼 감소한다는 것을 알 수 있습니다. 4번 단계에 들어가기 위한 조건은
\[ |I^\prime| + |J^\prime| < n\]
이었으므로, 식 1과 함께 식 2가 0보다는 항상 크다는 사실을 이끌어낼 수 있습니다. 앞에서 우리는 4번 단계가 끝나도 행렬의 모든 원소가 0보다는 크거나 같다고 하였는데 이번에는 모든 원소의 합이 감소하기만 한다는 것을 알았으니 결국 최악의 경우에는 모든 원소가 0이 되는 상황이 발생할 것이고 자명하게도 언젠간 4번 단계를 탈출할 것입니다. 물론, 모든 원소가 0이 되기 전에 탈출할 수도 있겠죠.
마치며
이번 시간에는 assignment problem과 Hungarian algorithm에 대해서 알아보았습니다. 특히, 이 알고리즘이 왜 optimal solution을 알려주는지에 대해서 좀 더 깊이 다루어 보았습니다. 아쉽게도 이 알고리즘이 다항 시간에 동작한다는 것을 보이지 못했습니다. 이에 관련하여 궁금하신 분은 다음 글을 읽어보시기 바랍니다.
2020/03/18 - [조합론적 최적화/Matching] - 헝가리안 알고리즘 시간 복잡도 분석
헝가리안 알고리즘 시간 복잡도 분석
지난번에 할당 문제와 헝가리안 알고리즘을 주제로 글을 작성하였습니다. 아래 링크를 참조하세요. 2019/08/07 - [조합론적 최적화/Matching] - 할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian A..
gazelle-and-cs.tistory.com
이 글에서는 헝가리안 알고리즘이 \( O(n^4) \)에 동작한다는 것을 보입니다. 알려진 바로는 \( O(n^3) \)에도 동작시킬 수 있다고 합니다만 개인적으로는 잘 모르겠습니다. 여기서 약간 뜯어 고쳐야 가능해 보입니다.
한 가지 더 말씀드리자면, 이 알고리즘은 LP duality를 통해서도 해석할 수 있습니다. 좀 더 자세히 말해서, 이 문제를 해결하는 linear program을 "잘" 만들면 각 행과 각 열에 빼는 값을 dual variable로 하는 dual program을 만들 수 있습니다. 이 때 행렬의 원소가 0이라는 의미는 dual의 constraint가 등식이 성립한다는 의미이고, 종국적으로는 complementary slackness를 사용하여 optimality를 증명할 수 있습니다. 처음 글을 적을 당시만 해도 이 부분까지 같이 다루어 보려고 했는데, 쓰고 보니 글이 너무 길어져서 이는 다음으로 미루어야 할 것 같네요.
지금 글을 마무리 짓는 때는 다행히도 에어컨이 고쳐졌습니다. '스카이'라고 부르는 중장비를 동원해서 얽히고 설킨 전선을 뚫고 기사님께서 실외기를 모두 수리해 주셨습니다. 평소에 그다지 에어컨을 켜고 살지는 않지만, 그래도 있으니 행복하군요. 이 행복함을 좀 누려야겠습니다.
참고로 다음 강의 자료를 주로 참조하였음을 밝힙니다.
https://resources.mpi-inf.mpg.de/departments/d1/teaching/ss11/OPT/lec11.pdf
감사합니다.
'조합론적 최적화 > Matching' 카테고리의 다른 글
| 텃의 정리 (Tutte's Theorem) (0) | 2020.10.10 |
|---|---|
| 헝가리안 알고리즘 시간 복잡도 분석 (7) | 2020.03.18 |
| 호프크로프트-카프 알고리즘 (Hopcroft-Karp Algorithm) (11) | 2020.02.22 |
| 쾨니그의 정리 (Kőnig's Theorem) (10) | 2019.01.28 |
| 홀의 정리 (Hall's Theorem) (8) | 2019.01.28 |



