엄청 오랜만에 포스팅을 합니다. 방학이 되면 시간이 나서 글을 좀 쓸 수 있을 줄 알았는데, 대학원생은 방학도 바쁘군요. 다행히 어느정도 일단락이 나서 이렇게 글을 쓸 수 있게 되었습니다. 개강 전에 한 두 개는 더 적을 수 있지 않을까 생각합니다.
반년에 글 하나씩 올리는 주제에 블로그를 운영한다고 말할 수 있으련지는 모르겠지만, 아무튼 블로그를 운영하면서 이제 슬슬 외부에도 노출이 되어가는 것을 보니 감회가 새롭습니다. 특히 제 블로그에서 가장 조회수가 높은 글은 헝가리안 알고리즘에 관한 글이었습니다.
할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian Algorithm)
이번 포스팅에서는 assignment problem과 Hungarian algorithm에 대해서 알아보겠습니다. 먼저 assignment problem이 어떤 것인지에 대해서 살펴보고, 이를 해결하는 방법을 알아보도록 하겠습니다. 인터넷을 찾아..
gazelle-and-cs.tistory.com
그렇게 많은 관심을 받을 줄은 잘 몰랐습니다. 다른 글에 비해 독보적인 조회수와 함께 댓글까지 달린 것을 보면, 말 다했죠. (허허) 아무래도 코딩 및 컴퓨터 과학을 좋아하시는 분들이라면 전반적으로 관심을 가질 내용이기도 하고, 특히 문제 해결 쪽을 좋아하시는 분들이라면 구현을 할 줄 아는데 왜 동작하는지 궁금해 하셔서 였으리라 생각합니다. 비록 저는 문제 해결 분야와는 좀 거리가 있는 사람이지만 말이죠.
이번에도 좀 비슷한 주제의 것을 가져왔습니다. 바로 Hopcroft-Karp algorithm입니다.[1] 영어 이름을 한글로 옮길 때는 참으로 어려운 것 같습니다. 제 생각에는 홉크로프트-카프가 되어야 하지 않을까 하는데, 한국어 위키피디아에는 내용이 없고, 네이버에서 검색했을 때는 몽땅 호프크로프트-카프로 나와서 저도 제목에 그냥 호프크로프트-카프로 적었습니다.
아무튼 이 알고리즘은 maximum bipartite matching을 \(O(n^{2.5})\) 시간에 해결하는 알고리즘으로 유명합니다. 이미 많은 분들이 이를 어떻게 구현하는지에 대해서 잘 정리해 놓으셨더군요. 하지만, 제가 이 알고리즘에 흥미를 갖게 된 이유는 따로 있습니다. 바로 시간복잡도입니다. 저는 지금껏 시간복잡도에 \(\log n\)이나 \(2^n\)같은 것은 봤어도, \(\sqrt{n}\)이 들어가는 것은 처음 봤습니다. 도대체 무슨 알고리즘에 어떤 분석을 해야 제곱근이 시간복잡도에 들어갈 수 있는지 너무 궁금했습니다. 이 포스트는 그 궁금증을 해소해 줄 것입니다.
기본 지식
들어가기에 앞서서 maximum matching에 관련된 잘 알려진 사실을 몇 가지 짚고 넘어가겠습니다. 혹시 관련된 내용을 잘 알고 계신다면, 이 절의 마지막에 기술된 알고리즘만 읽으시고 바로 다음 절로 넘어가셔도 무방합니다.
먼저, maximum matching problem은 어떤 (가중치가 없는) 그래프 \(G = (V, E)\)가 주어졌을 때, 여기서 크기가 가장 큰 matching을 찾는 문제입니다. 여기서 matching이란 끝점을 공유하지 않는 간선의 집합을 의미합니다. 좀 더 자세한 내용이 필요하시면, 제가 이전에 적은 포스트를 참조하시면 좋겠습니다.
2019/01/28 - [조합론적 최적화/Bipartite matching] - 쾨니그의 정리 (Kőnig's Theorem)
쾨니그의 정리 (Kőnig's Theorem)
이 글은 홀의 정리 (Hall's Theorem)와 밀접한 연관이 있습니다. 필요한 경우에는 이를 참조하세요. 2019/01/28 - [조합론적 최적화] - 홀의 정리 (Hall's Theorem) 무언가를 최적화시키는 문제를 보면 생각보다..
gazelle-and-cs.tistory.com
시작하기에 앞서, 아래의 내용은 꼭 bipartite graph가 아니어도 성립한다는 점을 밝힙니다. (비록 그림 예시는 bipartite grpah이기는 하지만 말이죠.)
어떤 matching \(M \subseteq E\)가 주어졌을 때, 어떤 정점이 \(M\)의 간선의 한 끝점을 이루면 그 정점을 matched 되었다고 부릅니다. 반대로, \(M\)의 어떤 간선에 의해서도 그 끝점이 되지 못하는 경우에는 그 정점이 exposed 되었다고 부릅니다. 또한, 그래프 위에서 \(M\)에 들어간 간선과 들어가지 않은 간선이 서로 교차하는 경로를 \(M\)에 대한 alternating path라고 합니다. 그러한 alternating path 중에서 양 끝점이 모두 exposed인 경우에는 특별히 \(M\)에 대한 augmenting path라고 부릅니다. 참고로 augmenting path의 길이는 항상 홀수입니다.

예를 들어보겠습니다. 위 그림에서 빨간 간선을 matching \(M\)에 포함된 간선이라고 하겠습니다. 그러면 정점 1, 4, 5, 7, 8, 10은 matched이고, 나머지 정점 2, 3, 6, 9는 exposed입니다.
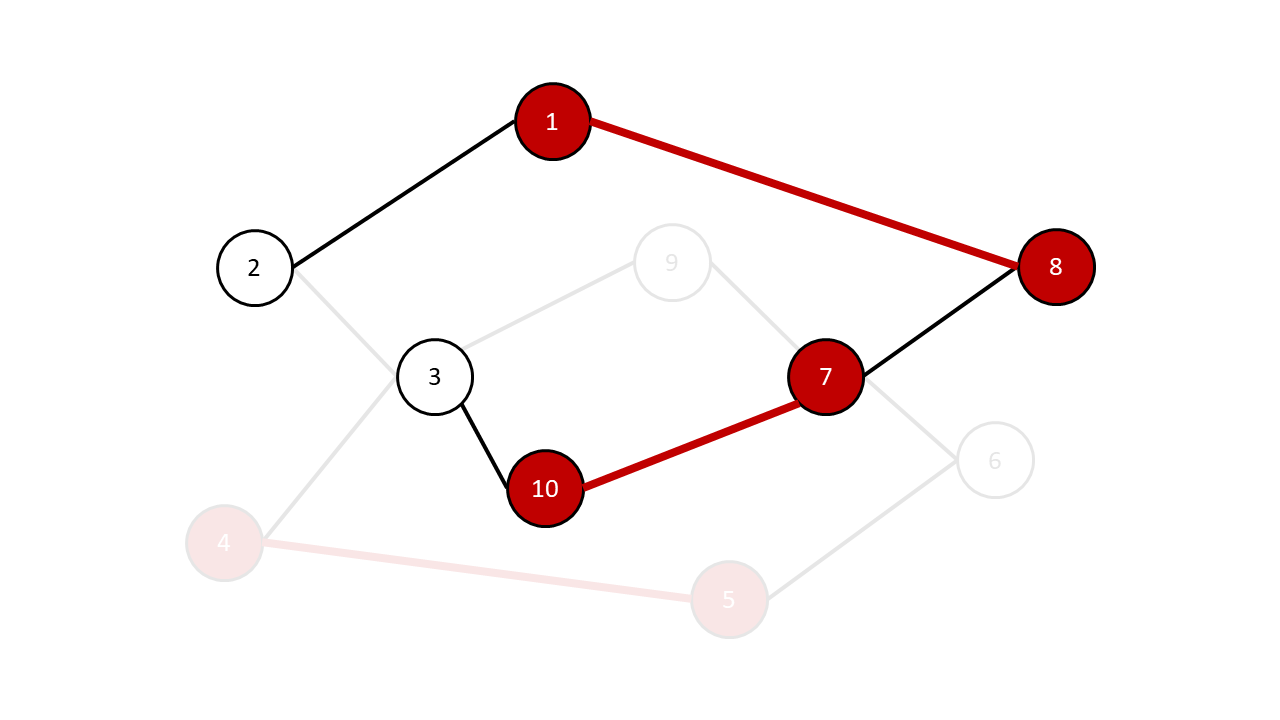
위 그림은 \(M\)에 대한 augmenting path 중 하나를 나타낸 것입니다. 자 이 그림을 잘 살펴보면, 우리가 왜 굳이 위와 같은 경로에다 augmenting path라는 특별한 이름을 붙였는지를 알 수 있습니다. 바로 이 경로를 따라서 \(M\)에 원래 들어가 있던 것은 빼고, \(M\)에 들어가 있지 않던 것은 넣어주면 새로운 matching을 얻을 수 있다는 점입니다. 그림 2의 경우에는 \((2, 1)\)을 넣고, \((1, 8)\)은 빼고, \((8, 7)\)은 넣고, \((7, 10)\)은 빼고, 마지막으로 \((10, 3)\)을 넣는 것이죠. 그러면 다음과 같은 matching을 얻게 됩니다.

이렇게 얻은 새로운 matching은 한 가지 흥미로운 성질이 있는데, 바로 기존의 matching보다 하나 더 많은 간선을 갖는 다는 것입니다. 이를 좀 더 엄밀히 정리해보도록 하겠습니다. 임의의 matching \(M\)과 그에 대한 augmenting path \(P\)가 주어졌을 때, 위에서 말한 \(P\)를 따라 \(M\)에 들어간 간선은 빼고 \(M\)에 없는 간선은 넣어주는 작업을 \(M \oplus P\)라고 지칭하겠습니다. 그러면 다음과 같은 성질을 만족합니다.
정리 1. Augmenting path의 성질
어떤 그래프 \(G = (V, E)\)에서 matching \(M\)과 그에 대한 augmenting path \(P\)가 주어졌다고 하자. 그러면 \(M \oplus P\)는 \(G\)의 또다른 matching이며 \(|M \oplus P| = |M| + 1\)을 만족한다.
정리 1의 엄밀한 증명은 생략하도록 하겠습니다. (사실 엄밀한 증명이라 할 것도 없어 보이긴 합니다.) 이 정리를 활용하여 얻을 수 있는 것은 maximum matching에는 augmenting path가 존재하지 않는다는 점입니다.
정리 2. Maximum matching과 augmenting path
어떤 matching \(M\)이 maximum matching일 필요충분조건은 \(M\)에 대한 augmenting path가 존재하지 않는다는 것이다.
증명은 간단합니다. 만약 augmenting path가 존재했다면, 정리 1에 의해서 \(M\)보다 크기가 더 큰 matching을 만들 수 있기 때문이죠. 반대로 augmenting path가 존재하지 않는 matching은 크기를 늘릴 수 있는 방법이 없으므로 maximum matching이 됩니다. 실례로 그림 3은 maximum matching입니다. 정점 6과 9를 잇는 augmenting path를 만들 수 없기 때문입니다.
지금까지 확인한 내용을 토대로 우리는 maximum matching을 구하는 간단한 알고리즘을 만들 수 있습니다.
알고리즘 1. 간단한 maximum matching 알고리즘
입력: 가중치가 없는 그래프 \(G = (V, E)\)
출력: Maximum matching
- \(M \gets \emptyset\)
- \(M\)에 augmenting path가 없을 때까지 다음을 반복한다.
- \(M\)에 대한 augmenting path 중 길이가 가장 짧은 path \(P\)를 구한다.
- \(M \gets M \oplus P\)
- \(M\)을 출력한다.
이 알고리즘의 correctnesss는 정리 2 덕분에 자명합니다. 시간복잡도는 굳이 분석하지 않겠습니다. 어차피 이를 분석하는 것이 우리의 주된 목표가 아니기 때문입니다.
대신 한 가지 질문을 드리죠. 왜 단계 2-1에서는 아무 augmenting path가 아닌 길이가 가장 짧은 것을 가지고 오는 것일까요? 사실 아무 augmenting path를 취해도 알고리즘의 correctness에는 문제가 없습니다. 하지만 가장 짧은 augmenting path를 선택하는 것은 앞으로 보여드릴 분석에 큰 영향을 미칩니다. 바로 이 알고리즘이 Hopcroft-Karp algorithm의 근간이기 때문이죠.
더 복잡하고 흥미로운 성질
이 절 제목에 어떤 이름을 붙일까 고민을 많이 했습니다만, 그냥 "더 복잡하고 흥미로운 성질"로 정했습니다. 작명 센스를 탓하고 싶지만, 이 절의 주제가 딱, 앞에서 다룬 기본적인 내용이 아닌 augmenting path에 관한 더 복잡하고 흥미로운, 더하여 Hopcroft-Karp algorithm을 증명하는 데 필수적인 성질을 알아보는 것이기 때문입니다.
시작하기 앞서, 위에서 슬쩍 넘어간 부분을 좀 더 집중적으로 보겠습니다. 바로 \(\oplus \)입니다. 사실 이는 대칭차(symmetric difference)를 의미했습니다. 즉, 임의의 두 간선 부분집합 \(S_1, S_2 \subseteq E\)에 대해서 \(S_1 \oplus S_2 \)은 \(S_1\)에만 있거나 \(S_2\)에만 있는 간선들의 집합을 의미합니다. 다시 쓰면, \(S_1 \oplus S_2 = (S_1 \setminus S_2)\cup(S_2 \setminus S_1)\)이 됩니다. 앞에서 임의의 matching \(M\)과 그에 대한 augmenting path \(P\)가 주어졌을 때 \(M \oplus P\)가 \(P\)를 간선의 집합으로 본다면 해당 동작이 대칭차의 정의에 부합한다는 것을 쉽게 알 수 있습니다.
이제부터 크게 두 가지 성질을 소개하고자 합니다. 첫 번째는 matching의 크기가 작으면 반드시 길이가 짧은 augmenting path가 존재한다는 것입니다.
정리 3. Matching의 크기와 augmenting path의 길이
어떤 그래프 위의 maximum matching의 크기를 \( \mathsf{OPT}\)라고 하자. 이 그래프 위의 임의의 matching \(M\)에 대하여, \(|M| < \mathsf{OPT}\)이면, 길이가 \(2 \left\lfloor \frac{|M|}{\mathsf{OPT} - |M|} \right\rfloor + 1\)을 넘지 않는 \(M\)에 대한 augmenting path가 존재한다.
증명은 생각보다 간단합니다. 같은 그래프 \(G = (V, E)\) 위 임의의 maximum matching \(M^\star\)를 하나 생각하겠습니다. 여기에다 정점 \(V\)는 그대로 두고 대신 간선은 \(M\)과 \(M^\star\)의 대칭차 \(M \oplus M^\star \)만 고려하겠습니다. Matching의 정의에 의해서 모든 정점은 최대 하나의 \(M\)에 포함된 간선과 \(M^\star\)에 포함된 간선에 인접합니다. 따라서 \(M \oplus M^\star\)는 정점을 공유하지 않는 순환들(cycles)과 경로들(paths)로 이루어져있다는 사실을 알 수 있습니다.
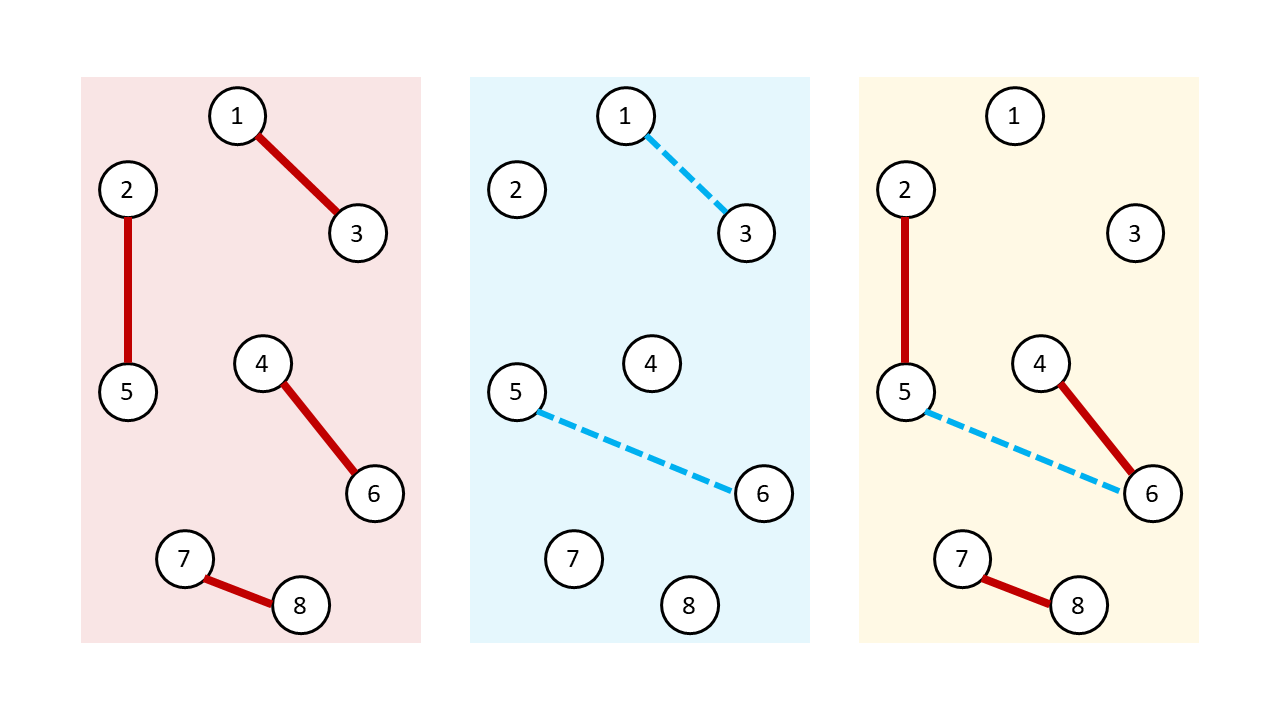
이 때, \(M\)의 크기가 \(M^\star\)보다 작으므로 분명히 적어도 \(|M^\star| - |M|\)의 개수만큼 서로 정점을 공유하지 않는 \(M\)에 대한 augmenting path가 존재한다는 것 또한 알 수 있습니다. \(M\)에는 \(|M|\)개의 간선이 있으므로 비둘기집 원리에 의해서 최소한 하나의 augmenting path는 \(M\)에 포함된 간선 \(\left\lfloor \frac{|M|}{|M^\star| - |M|} \right\rfloor\)개와 \(M^\star\)에 포함된 간선 \(\left\lfloor \frac{|M|}{|M^\star| - |M|} \right\rfloor + 1\)개로 이루어져 있을 것입니다. 이 augmenting path가 곧 정리를 만족하는 augmenting path가 됩니다.
다음 성질은 알고리즘 1이 매번 굳이 가장 짧은 augmenting path를 선택하는 이유를 설명하는데 필요합니다.
정리 4. 가장 짧은 augmenting path의 성질
임의의 matching \(M\)에 대해 가장 짧은 augmenting path를 \(P\)라고 하자. 그러면, 새로운 matching \(M \oplus P\)에 대한 임의의 augmenting path \(P^\prime\)에 대해 \(|P^\prime| \geq |P| + 2 |P \cap P^\prime| \)을 만족한다.
이 부분 증명은 약간 복잡할 수 있습니다. 하지만, 이 정리는 이번 글에서 가장 중요한 정리 중 하나이기 때문에 아래에 증명을 밝히도록 하겠습니다. 먼저, matching \(M \oplus P \)에 \(P^\prime\)을 덧댄 새로운 matching을 \(M^\prime\)이라고 하겠습니다. 즉, \(M^\prime := M \oplus P \oplus P^\prime \)입니다. 먼저, 정리 1에 의하여 \( |M^\prime| = |M| + 2 \)라는 사실을 얻을 수 있습니다. 또, 위 정리의 증명에서 처럼 \(M \oplus M^\prime \)에는 정점을 공유하지 않는 \(M\)에 대한 augmenting path가 적어도 두 개 존재합니다. 조건에서 \(P\)는 \(M\)에 대한 augmenting path 중 가장 짧기 때문에, 이를 조합하면 \[ |M \oplus M^\prime| \geq 2|P| \tag{1} \]를 얻을 수 있습니다. 또한, 대칭차의 정의 및 성질을 잘 활용하면 \(M \oplus M^\prime = M \oplus M \oplus P \oplus P^\prime = P \oplus P^\prime \)이라는 사실을 얻을 수 있습니다. (\(M \oplus M = \emptyset\)이라는 사실을 이용하면 됩니다.) 이를 토대로 대칭차의 정의를 다시금 사용하면 \[ |M \oplus M^\prime| = |P \oplus P^\prime| = |P| + |P^\prime| - 2 |P \cap P^\prime| \tag{2} \]라는 점을 이끌어낼 수 있습니다. 식 (1)과 (2)를 활용하면 정리의 식을 증명할 수 있습니다.
알고리즘 및 분석
드디어 이번 절에서 Hopcroft-Karp algorithm이 무엇인지 설명하도록 하겠습니다. 사실 Hopcroft-Karp algorithm은 앞에서 소개한 간단한 알고리즘에 약간의 "양념"을 첨가한 것입니다. 따라서, 이 요리의 베이스는 알고리즘 1에서 시작됩니다. 알고리즘 1이 총 \(k\)번의 반복했다고 가정하겠습니다. 여기서 \(i\) 번째 반복할 때 단계 2-1에서 얻은 augmenting path를 \(P_i\)라고 하고, 단계 2-2에서 \(P_i\)를 적용하여 얻은 새로운 matching을 \(M_i\)라고 하겠습니다. 자연스럽게 \(M_0\)는 단계 1에서 정해 준 공집합으로 정의하겠습니다. 참고로, 정리 1에 의해서, 모든 \(i = 0, \cdots, k\)에 대해 \(|M_i| = i\)를 만족하며 \(k\)는 최적값, 즉 maximum matching의 크기가 됩니다.
그러면 우리는 위 절에서 증명한 정리들을 통해 다음과 같은 정리들을 이끌어낼 수 있습니다.
정리 5. Augmenting path 길이의 단조 증가 성질
모든 \(i = 1, \cdots, k - 1 \)에 대해, \(|P_i| \leq |P_{i + 1}|\)
정리 5가 의미하는 바는 만약 우리가 매 반복마다 가장 짧은 augmenting path를 선택하면 그 길이는 계속 길어지기만 할 뿐이라는 것입니다. 증명은 정리 4에서 \(P\) 자리에 \(P_i\), \(P^\prime\) 자리에 \(P_{i + 1}\)을 넣으면 쉽게 보일 수 있습니다.
다음 정리는 드디어 왜 시간복잡도에 제곱근이 들어가는지를 알려줍니다.
정리 6. 서로 다른 길이의 수
\(|P_1|, |P_2|, \cdots, |P_k|\) 중 서로 다른 숫자의 개수는 \(2 \lfloor \sqrt{k} \rfloor + 2\)보다 작거나 같다. 즉, \[\left| \left\{ |P_1|, |P_2|, \cdots, |P_k| \right\} \right| \leq 2 \left\lfloor \sqrt{k} \right\rfloor + 2 \]를 만족한다.
이를 증명해 보도록 하겠습니다. 먼저 \(t := \lfloor k - \sqrt{k} \rfloor\)라고 하겠습니다. 그러면, \(|M_t| = t \)라는 점과 정리 3을 통해서 \[ |P_{t + 1}| \leq 2 \left\lfloor \frac{\lfloor k - \sqrt{k} \rfloor}{k - \lfloor k - \sqrt{k} \rfloor} \right\rfloor + 1 \leq 2 \lfloor \sqrt{k} \rfloor + 1\]임을 알 수 있습니다. 따라서, 정리 5에 의해 \[|P_1| \leq |P_2| \leq \cdots \leq |P_t| \leq |P_{t + 1}| \leq 2 \lfloor \sqrt{k} \rfloor + 1\]임을 알 수 있으며, 이를 통해 \( |P_1|, \cdots, |P_t| \)는 각각 \( 2 \lfloor \sqrt{k} \rfloor + 1 \)보다 작거나 같은 \( \lfloor \sqrt{k} \rfloor + 1 \) 개의 홀수 중 하나라는 사실을 얻을 수 있습니다. 반대로 \(|P_{t + 1}|, \cdots, |P_k|\)의 총 개수는 \( k - t = \lceil \sqrt{k} \rceil \)이므로 최대 그만큼의 서로 다른 숫자를 이룰 수 있습니다. 따라서 서로 다른 숫자의 총 개수는 아무리 많아도 \[\lfloor \sqrt{k} \rfloor + 1 + \lceil \sqrt{k} \rceil \leq 2 \lfloor \sqrt{k} \rfloor + 2\]가 됩니다.
마지막 정리는 길이가 같은 augmenting path는 동시에 구하여 적용해도 괜찮다는 사실을 알려줍니다.
정리 7. 같은 길이의 augmenting path의 성질
임의의 서로 다른 \(i, j\)에 대해서, \(|P_i| = |P_j| \)이면 \(P_i\)와 \(P_j\)는 정점을 공유하지 않는다.
이 정리도 정리 4를 활용하면 쉽게 보일 수 있습니다. 일단, \(i < j\)라고 가정하겠습니다. 만약 \(P_i\)와 \(P_j\)가 정점을 공유한다면 \(i, j\) 사이의 어떤 \(s\)에 대해 \(P_s\)와 \(P_{s + 1}\)이 정점을 공유할 것입니다. 그러면 정리 4에 의해서 \[ |P_{s + 1}| \geq |P_s| + 2 |P_s \cap P_{s + 1}| > |P_s| \]이 됩니다.[2] 하지만, 정리 5에 의해서 \(|P_i| = |P_s| = |P_{s + 1}| = |P_j|\)이므로 모순이 됩니다.
증명에 오류가 있어 다시 적습니다. 먼저, \(i < j\)라고 가정하겠습니다. 이제 다음을 만족하는 \(i'\), \(j'\)을 생각해 보겠습니다.
- \(i \leq i' < j' \leq j\).
- 임의의 \(s = i'+1, \ldots, j'-1\)에 대해, \(P_s\)가 \(P_{i'}\)과도 정점을 공유하지 않고, \(P_{j'}\)과도 정점을 공유하지 않는다.
그러면 두 번째 조건에 의해 \(P_{j'}\)이 \(M \oplus P_{i'}\)의 augmenting path가 된다는 것을 알 수 있습니다. 여기에 정리 4를 적용하면, \[ |P_{j'}| \geq |P_{i'}| + 2|P_{i'} \cap P_{j'}| > |P_{i'}| \]을 이끌어 낼 수 있습니다.[2] 하지만 이는 정리 5에 의해 \( |P_i| = |P_{i'}| = |P_{j'}| = |P_j| \)를 만족하므로 모순입니다.
드디어, Hopcroft-Karp algorithm을 소개할 시간이 다가왔습니다.
알고리즘 2. Hopcroft-Karp algorithm
입력: 가중치가 없는 그래프 \(G = (V, E)\)
출력: Maximum matching
- \(M \gets \emptyset\)
- \(M\)에 augmenting path가 없을 때까지 다음을 반복한다.
- \( \ell \gets \) \(M\)에 대한 augmenting path 중 가장 짧은 것의 길이
- 길이가 \(\ell\)이고 서로 정점을 공유하지 않는 \(M\)에 대한 augmenting path를 최대로 찾는다. 이를 \(Q_1, \cdots, Q_t\)라고 하자.
- \(M \gets M \oplus Q_1 \oplus \cdots \oplus Q_t \)
- \(M\)을 출력한다.
네, 알고리즘 1과 매우 흡사합니다. 사실 알고리즘 2에서 단계 2-3을 한 번에 쓰지 않고 따로 적었다면 알고리즘 1과 동일합니다. 다른 점이라면, 정리 5에 의해서 augmenting path의 길이가 짧아지지 않으며, 같은 길이의 augmenting path는 정리 7에 의해 서로 정점을 공유하지 않을 것이기 때문에 단계 2를 통해 그러한 경로들을 한 번에 찾는 것이죠. 게다가 서로 다른 길이의 개수는 최대 \(2 \lfloor \sqrt{k} \rfloor + 2 = O(\sqrt{n})\)이므로, 단계 2를 빠른 시간에 처리할 수 있다면 시간을 단축하게 됩니다. 정리하면 다음과 같습니다.
정리 8. Hopcroft-Karp algorithm
주어진 그래프 \(G = (V, E)\)에 대해, \(n := |V|\), \(m := |E|\)라고 하자. 만약, 알고리즘 2의 단계 2를 \( f(n, m)\)의 시간복잡도로 해결할 수 있다고 하자. 그러면 알고리즘 2는 \(O(f(n, m) \cdot \sqrt{n})\)의 시간 동안 maximum matching problem을 해결하는 알고리즘이다.
마치며
이 글에서는 Hopcroft-Karp algorithm에 대해 알아보았습니다. 정리 8에서 주목할 점은 알고리즘 2가 기술된 것에 따르면 주어진 그래프가 꼭 bipartite graph일 필요는 없다는 것입니다. 하지만 우리는 대개 Hopcroft-Karp algorithm이 bipartite graph에서 \(O(n^{2.5})\)의 시간에 maximum matching을 구하는 것으로 알고 있습니다. 그 이유는 바로, \(G\)가 bipartite graph이면, \(f(n, m) = O(n + m)\)으로 만들 수 있기 때문입니다.
간단히 설명드리면, 주어진 bipartite graph \(G = (V_L \cup V_R, E)\)와 현재의 matching \(M \subseteq E\)에 대해서 모든 정점을 그 정점에서 \(V_R\)의 아무 exposed된 정점까지 \(M\)에 대한 alternating path로 도달할 수 있는 최단 길이에 따라서 partition할 수 있습니다. 이렇게 partition된 그래프에 대해 DFS를 잘 사용하면 됩니다. 하지만, 이 부분은 이 포스트에서 다룬 내용에 비해 (개인적으로는) 상대적으로 재미도 없고, 많은 분들이 잘 설명해 놨다고 생각해서 생략하도록 하겠습니다.
이 알고리즘 및 여기서 보인 많은 정리들은 이후 maximum matching problem을 이해하는 데 큰 영향을 주었습니다. 개인적으로도 이번 기회에 이를 모두 정리할 수 있어서 만족합니다. 다른 포스트에 비해서 그림보다 글이 많은 것 같기도 한데, 모쪼록 이해가 되셨기를 바랍니다.
궁금하신 점이나 질문하실 것이 있으면 댓글 남겨주세요. 고맙습니다.
참조 및 주석
[1] John E. Hopcroft and Richard M. Karp. "An \(n^{5/2}\) algorithm for maximum matchings in bipartite graphs." SIAM Journal on computing 2.4 (1973): 225-231.
[2] 사실 \(P_s\)와 \(P_{s + 1}\)이 정점을 공유한다는 사실이 곧바로 \(|P_s \cap P_{s + 1}| > 0\)을 이끌어내지는 않습니다. 이는 두 경로가 augmenting path이기 때문에 성립합니다. 엄밀히 말하면 다음과 같습니다. 만약 \(v \in V\)를 \(P_s\)와 \(P_{s + 1}\)이 공유하는 정점이라고 하겠습니다. 그러면 \(v\)는 분명히 \(M_s := M_{s-1} \oplus P_s\)의 한 간선 \(e\)에 인접할 겁니다. \(P_{s + 1}\)은 \(M_s\)의 한 augmenting path이고 \(v\)를 지나므로 반드시 \(e\)를 지나야 합니다.
'조합론적 최적화 > Matching' 카테고리의 다른 글
| 텃의 정리 (Tutte's Theorem) (0) | 2020.10.10 |
|---|---|
| 헝가리안 알고리즘 시간 복잡도 분석 (7) | 2020.03.18 |
| 할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian Algorithm) (38) | 2019.08.07 |
| 쾨니그의 정리 (Kőnig's Theorem) (10) | 2019.01.28 |
| 홀의 정리 (Hall's Theorem) (8) | 2019.01.28 |



