우리에게 처리해야 할 작업들이 있다고 해 보겠습니다. 다만 작업들은 처음부터 주어지지 않고 시간이 흐르면서 하나씩 도착합니다. 작업을 처리하기 위해 우리는 최대 하나의 작업을 할당받을 수 있는 기계를 몇 대 갖고 있습니다. 문제는 각 작업마다 해당 작업을 처리할 수 있는 기계가 따로 정해져 있다는 것이며, 심지어 어느 기계에서 처리될 수 있는지는 해당 작업이 도착해야 알 수 있다는 점입니다. 우리는 매번 작업이 도착할 때마다 이 작업을 어떤 기계에 할당할지, 그리고 만약 할당한다면, 어느 가용한 기계에 할당하여 줄지를 바로 결정하여야 합니다. 여기서 어려운 점은 이 결정을 후일 번복할 수 없다는 것입니다. 이런 환경에서 작업이 모두 도착했을 때 최대한 많은 작업을 처리하는 것이 목표입니다. 이는 유명한 온라인 최적화 문제 중 하나인 온라인 이분 매칭 문제(online bipartite matching problem)를 나타낸 것으로, 그동안 저는 제 블로그에서 여러 번 이 문제를 다룬 바 있습니다.
그런데 만약 작업을 쪼개어 여러 기계에 할당할 수 있다면 어떻게 될까요? 예를 들어, 어떤 작업이 도착했을 때, 0.2 조각은 첫 번째 기계에, 0.3 조각은 두 번째 기계, 나머지 0.5 조각은 세 번째 기계에 나누어 할당할 수 있는 것입니다. 또한 각 기계는 할당 받은 작업 조각들의 합이 1을 넘지만 않으면 되는 것이고요. 작업을 조각내는 것이 찜찜하다면, 한 작업이 만 개의 동일한 세부 작업으로 이루어져 있고, 각 기계도 최대 만 개의 세부 작업을 할당 받을 수 있는 상황으로 보셔도 무방합니다. 이 문제를 우리는 온라인 분수 이분 매칭 문제(online fractional bipartite matching problem)라고 부릅니다. 구분을 위해 작업을 쪼갤 수 없는 원래 문제는 온라인 정수 이분 매칭 문제(online integral bipartite matching problem)라고도 부릅니다.
지난 포스트에서 우리는 온라인 정수 이분 매칭 문제를 해결하는 경쟁 알고리즘들을 공부하였습니다. 특히, 1/2의 경쟁비를 갖는 결정론적 알고리즘과 \(1-1/e\)의 경쟁비를 갖는 랜덤 알고리즘을 배웠죠. 온라인 분수 이분 매칭 문제에서는 알고리즘이 더 높은 자유를 가지므로 더 좋은 경쟁비의 알고리즘을 기대할 수 있겠습니다. 실지로 이번 포스트에서는 분수 매칭 문제를 \(1-1/e\)의 경쟁비로 해결하는 결정론적 알고리즘을 소개합니다.
문제 정의
문제의 입력은 어떤 이분 그래프(bipartite graph) \(G = (L \cup R, E)\) 위에서 정의됩니다. 편의 상 \(L\)의 각 정점을 기계, \(R\)의 각 정점을 작업이라고 부르겠습니다. 만약 어떤 작업 \(j \in R\)가 어떤 기계 \(i \in L\)에 할당될 수 있을 때, 두 정점 사이에 간선 \((i, j) \in E\)가 존재합니다. 기계는 처음부터 모두 알려지는 반면, 작업은 하나씩 입력됩니다.
어떤 작업 \(j \in R\)가 들어왔을 그때에서야 우리는 \(j\)가 할당될 수 있는 기계가 무엇인지 알 수 있습니다. 작업 \(j\)에 인접한(adjacent) 기계를 \(N(j)\), 딸린(incident) 간선들을 \(\delta(j)\)라고 부르겠습니다. 우리는 1의 작업량을 갖는 작업 \(j\)를 쪼개어 인접한 기계에 나누어 할당해 주려고 합니다. 다시 말해, 인접한 기계 \(i \in N(j)\)에 할당된 조각의 양을 \(x_{(i,j)}\)라고 한다면, \[ \sum_{e \in \delta(j)} x_e \leq 1 \]을 만족해야 하겠습니다. 이번 작업 \(j\)에 대해 \(\{x_e\}_{e \in \delta(j)}\)가 결정된 후에는 이 값을 변경할 수 없습니다. 각 기계 또한 도합 최대 1의 작업량을 할당받을 수 있습니다. 따라서 각 \(i \in L\)에 대해 어느 순간에서든지 \[ \sum_{e \in \delta(i)} x_e \leq 1 \]을 만족해야 합니다. 여기서 \(\delta(i)\)는 앞에서 정의한 것과 유사하게, 기계 \(i\)에 딸린 간선들을 의미합니다. 우리의 목표는 최대한 많은 양의 작업을 처리하는 것입니다. 이는 각 간선에 할당된 작업 조각의 양을 최대화하는 것과 같습니다.
이를 선형 계획법으로 나타내면 아래와 같습니다.
\[ \begin{array}{rll} \text{maximize } & \displaystyle \sum_{e \in E} x_e \\ \text{subject to } & \displaystyle \sum_{e \in \delta(i)} x_e \leq 1, & \forall i \in L, \\ & \displaystyle \sum_{e \in \delta(j)} x_e \leq 1, & \forall j \in R, \\ & x_e \geq 0, & \forall e \in E. \end{array} \]
이 LP를 활용하여 문제를 다시 이해해 보겠습니다. 처음에는 알려진 정점이 없고, 각 기계에 가해진 첫 번째 제약 조건만 존재합니다. 매 시각 어떤 작업 \(j\)가 들어오면, \( \delta(j) \)가 알려집니다. 그러면 첫 번째 제약 조건은 해당 변수들이 추가되는 방식으로 갱신되고, 두 번째 제약 조건은 해당 \(j\)의 것이 통째로 추가되는 방식으로 갱신됩니다. 이때 우리는 다음 작업이 들어오기 전에 \(\{x_e\}_{e \in \delta(j)}\)의 값을 결정해 주어야 합니다. 이 결정은 이후 번복될 수 없습니다.
물 채우기 알고리즘(water-filling algorithm)
이제 알고리즘을 생각해 보겠습니다. 작업을 쪼갤 수 있기 때문에 가장 쉽게 생각할 수 있는 알고리즘은 역시 균등하게 쪼개서 기계에 할당해 주는 방법이겠습니다. 다시 말해, 작업 \(j\)가 입력되었을 때, 각 \(e \in \delta(j)\)에 대해, \(x_e = 1/|N(j)|\)로 두는 것이죠. 하지만 이 알고리즘은 1/2보다 좋은 경쟁비를 가질 수 없습니다. 다음의 입력을 생각해 봅시다. 이 입력은 이전 글에서도 사용된 바 있습니다.
온라인 이분 매칭 (Online Bipartite Matching)
어떤 그래프에서 서로 정점을 공유하지 않는 간선의 부분집합을 우리는 매칭(matching)이라고 부릅니다. 매칭의 모양을 살펴보면, 각 정점이 최대 하나의 다른 정점과 짝지어진 꼴입니다. 이를 통
gazelle-and-cs.tistory.com
- \(L_1 := \{i_1, \ldots, i_d\}\), \(L_2 := \{i_{d+1}, \ldots, i_{2d}\}\), \(L := L_1 \cup L_2\).
- \(R_1 := \{j_1, \ldots, j_d\}\), \(R_2 := \{j_{d+1}, \ldots, j_{2d}\}\), \(R := R_1 \cup R_2\).
- \(k \in \{1, \ldots, d\}\)에 대해, \(N(j_k) := \{i_k\} \cup L_2\).
- \(k \in \{d +1, \ldots, 2d\}\)에 대해, \(N(j_k) := \{i_k\}\).
- \(R_1\)이 모두 입력된 후 \(R_2\)가 입력된다.
\(R_1\)이 모두 들어왔을 때를 생각해 보겠습니다. 이 알고리즘은 각 작업 \(j\)를 \(d+1\) 등분 낸 후 각 기계에 할당하므로, \(L_1\)의 각 기계는 \(\frac{1}{d+1}\)씩의 작업 조각을, \(L_2\)의 각 기계는 \(\frac{d}{d + 1}\)씩의 작업 조각을 할당 받게 됩니다. 따라서 \(R_2\)의 각 작업들은 자신이 할당될 수 있는 유일한 기계에 최대 \(\frac{1}{d+1}\)의 작업 조각만 할당시킬 수 있습니다. 그러므로 모든 작업이 도착한 후 알고리즘이 할당시킨 작업의 총합은 \(d + \frac{d}{d + 1} < d + 1\)이 됩니다. 최적해에서는 모든 작업을 할당시킬 수 있으므로, 이 알고리즘의 경쟁비는 \(\frac{d + 1}{2d} \to \frac{1}{2}\)을 넘지 못합니다.
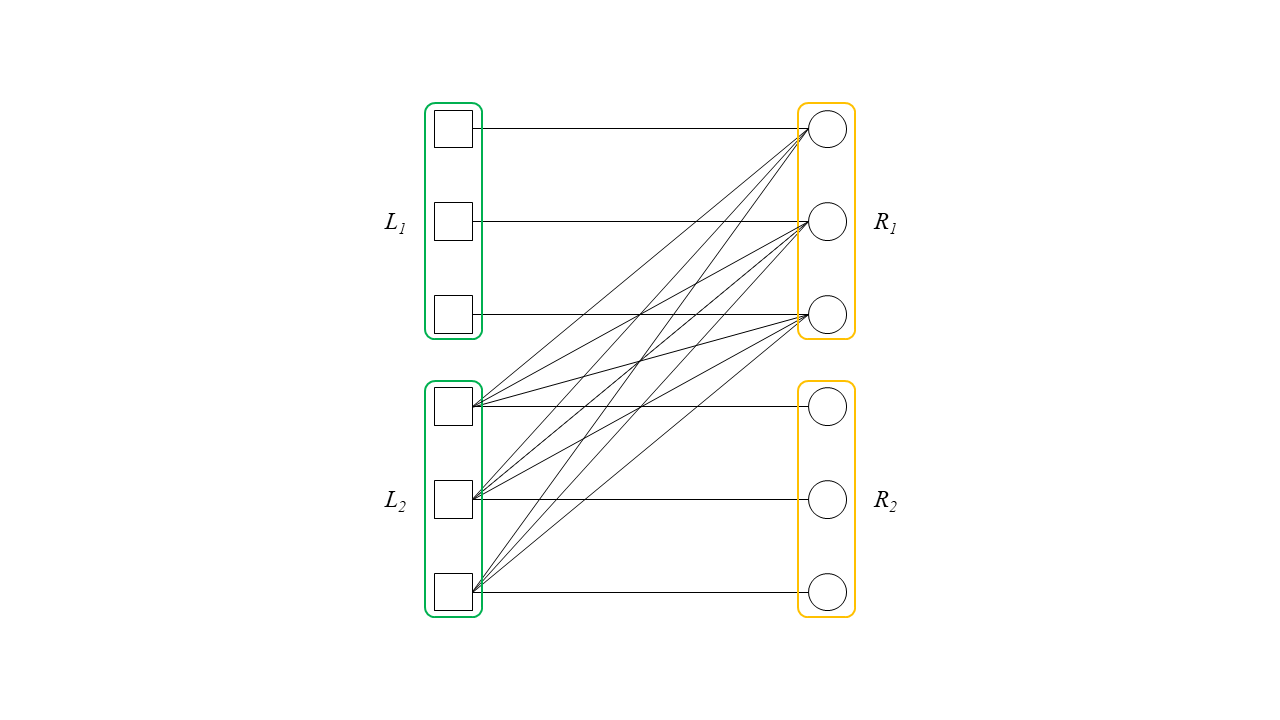
이러한 상황이 발생한 원인은 무엇일까요? 바로 \(L_1\)의 기계보다 \(L_2\)의 기계에 너무 많은 작업을 할당했기 때문입니다. \(R_1\)의 작업이 들어올 때마다 \(L_1\)의 기계에는 \(\frac{1}{d+1}\)의 부하만 생기는데 반해 \(L_2\)의 기계는 부하가 계속 증가하는 것을 확인하시기 바랍니다. 하지만 알고리즘은 이 현상을 무시하고 \(R_1\)의 작업을 인접한 기계에 균등하게 분배합니다.
따라서 작업을 할당하는 보다 자연스러운 방법은 부하가 적은 기계부터 차곡차곡 작업 조각을 할당하여 인접한 기계들이 최대한 동일한 부하를 받도록 하는 것이겠습니다. 어떻게 하면 이 목표를 달성할 수 있을지 예시와 함께 알아 보겠습니다. 어떤 작업이 하나 도착했을 때를 생각해 봅시다. 이 작업이 할당될 수 있는 기계들의 그동안 할당 받은 작업량이 다음 그림과 같이 주어졌다고 해 보겠습니다.
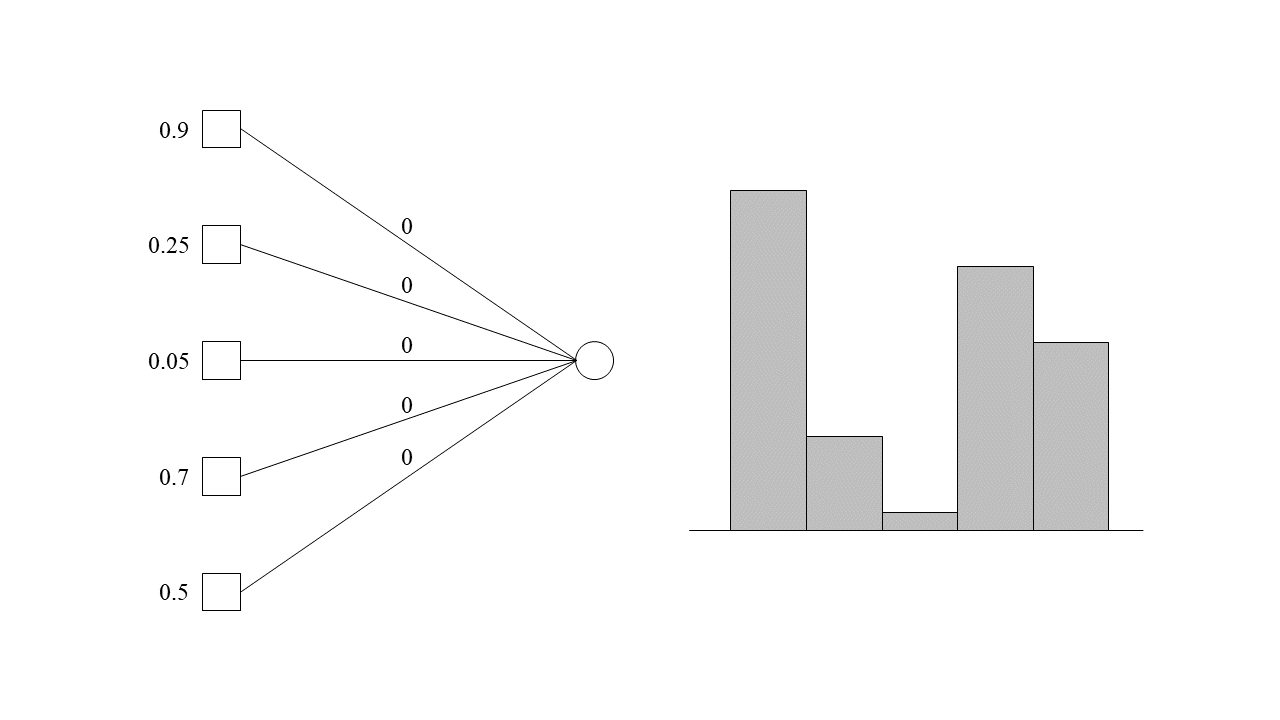
우리의 목표는 인접한 기계들이 최대한 동일한 부하를 받도록 작업을 할당하는 것입니다. 이를 위해 가장 부하가 적은 기계부터 차츰차츰 작업을 할당시켜 보도록 하겠습니다. 현재 세 번째 기계가 가장 적은 0.05의 작업을 받은 상태이므로 세 번째 기계에다가 작업을 할당해 봅시다. 만약 0.1 조각만큼을 할당한다면 아래와 같은 모습이 될 것입니다.
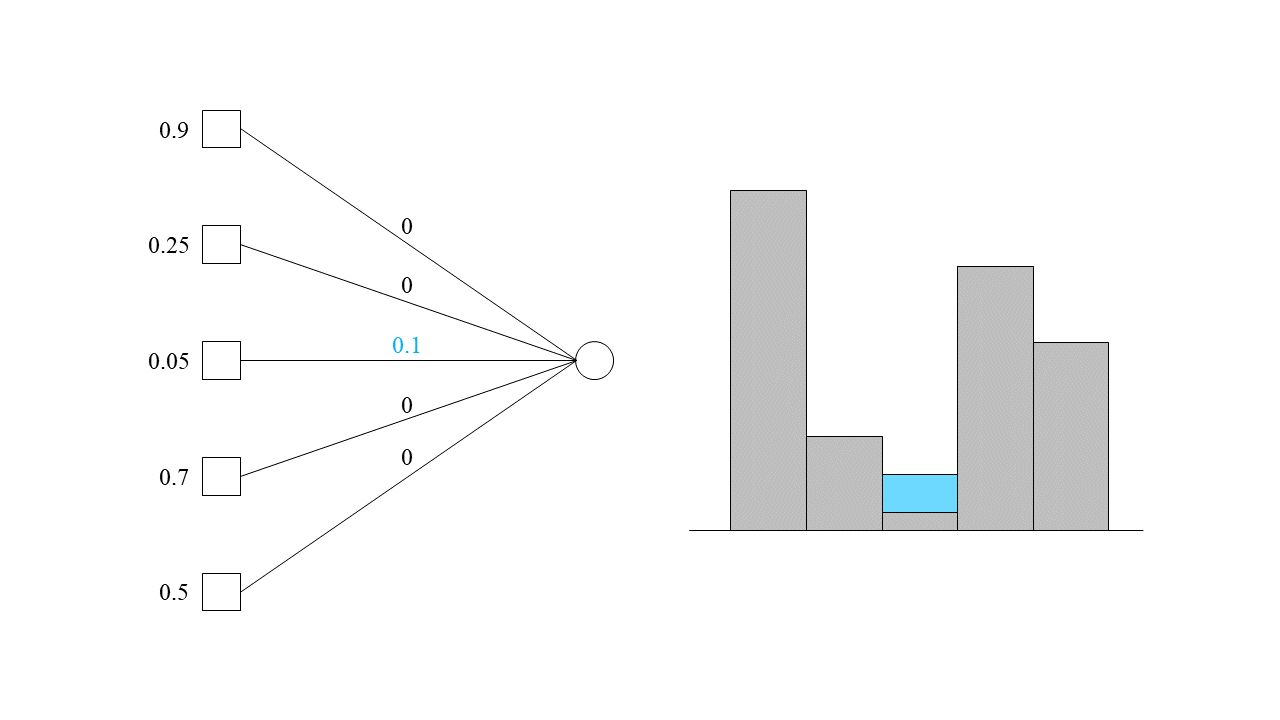
여전히 세 번째 기계가 가장 적은 부하를 받고 있으므로, 세 번째 기계에 계속해서 작업을 할당시켜 보겠습니다. 도합 0.2의 조각이 세 번째 기계에 할당되었을 때를 생각해 보겠습니다.
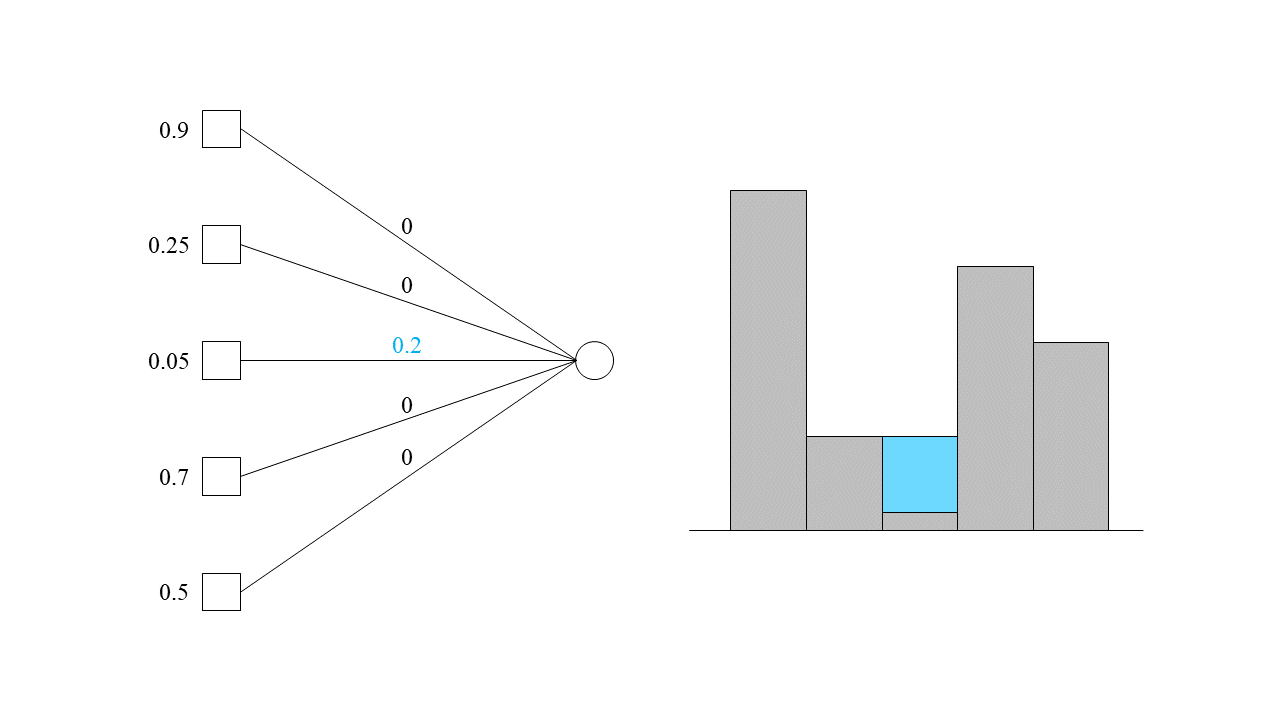
이제 세 번째 기계의 부하가 0.25가 되어 두 번째 기계가 받는 부하와 동일해졌습니다. 여전히 우리는 0.8의 작업 조각이 남아있습니다. 이제부터는 어떻게 작업을 할당해 주는 것이 바람직할까요? 두 번째와 세 번째 기계에 동시에 할당하는 것이 자연스러운 선택일 것입니다. 예를 들어, 이때로부터 두 번째와 세 번째 기계에 0.1씩을 더 할당해 준다면 아래와 같은 모습일 것입니다.
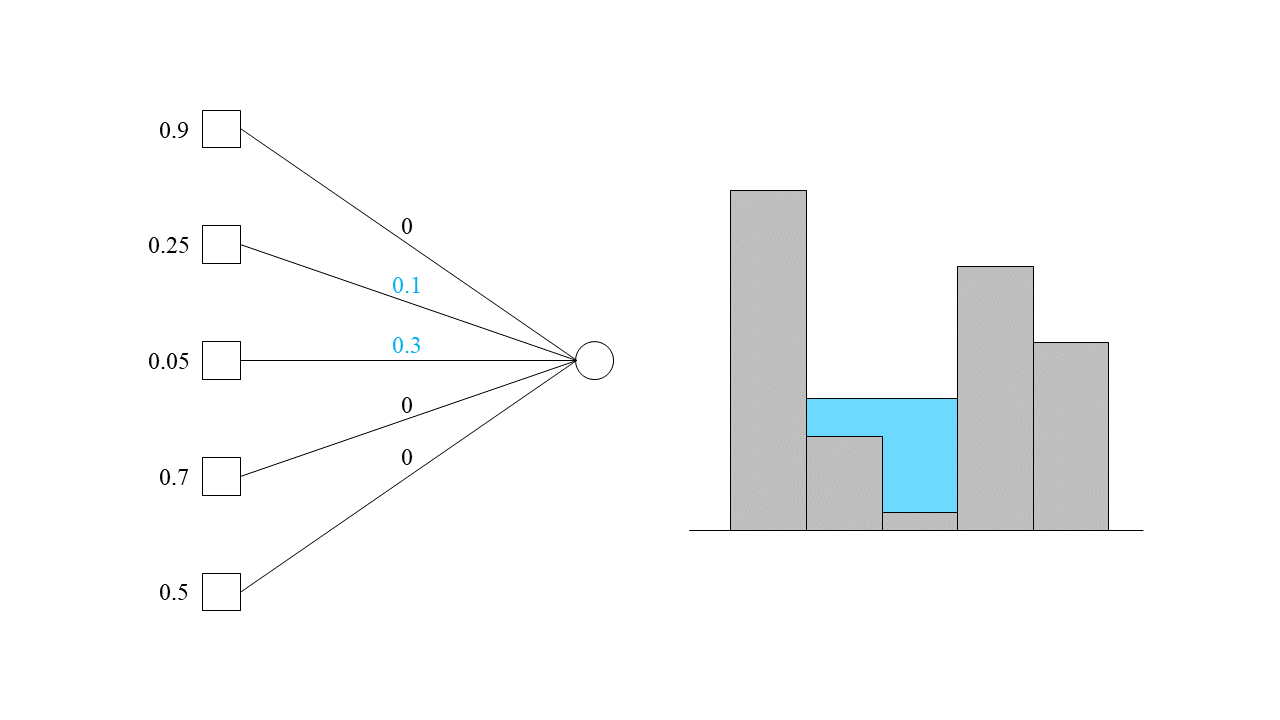
같은 이치로 두 번째와 세 번째 기계에 작업을 할당시키다 보면 언젠가 총 부하가 다섯 번째 기계와 동일해지는 때가 옵니다.
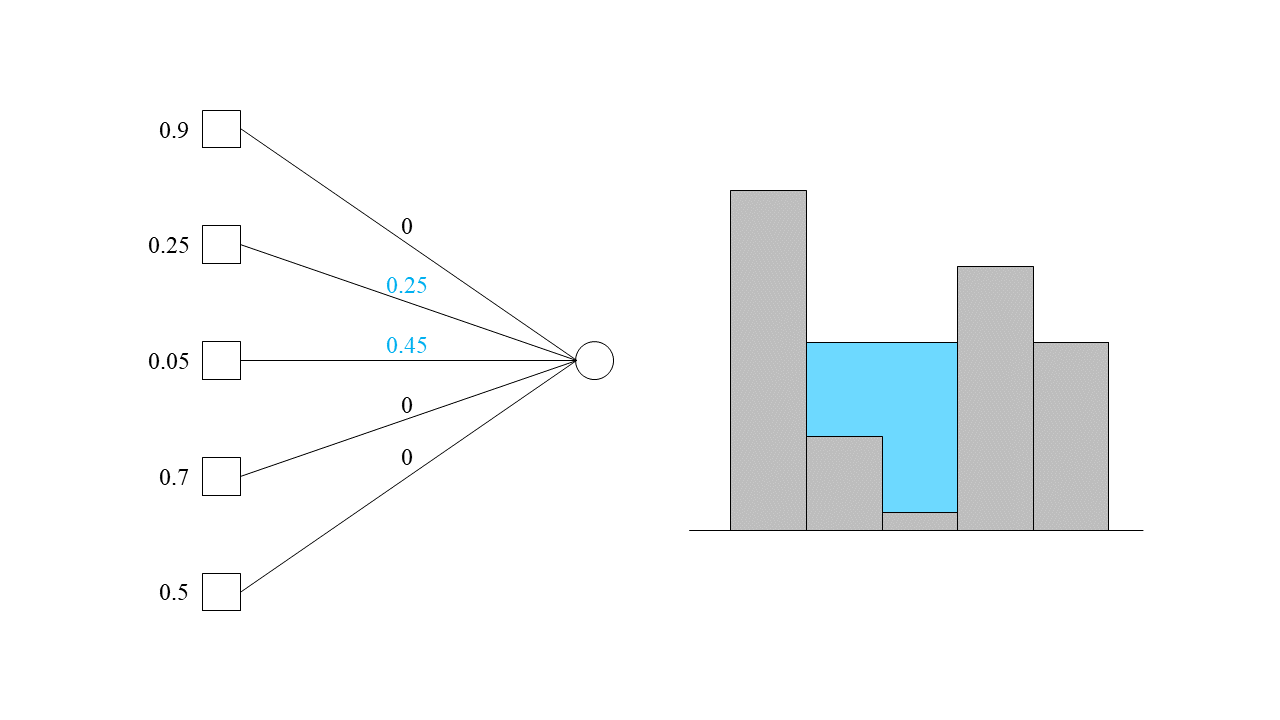
현재까지 총 0.7의 작업을 할당해 주었으므로, 여전히 0.3이 남은 상태입니다. 이제부터는 자연스럽게 두 번째, 세 번째, 그리고 다섯 번째 기계에까지 작업을 동시에 할당해 주도록 하겠습니다. 그러면 아래 상태일 때 1의 작업을 모두 할당하게 됩니다.
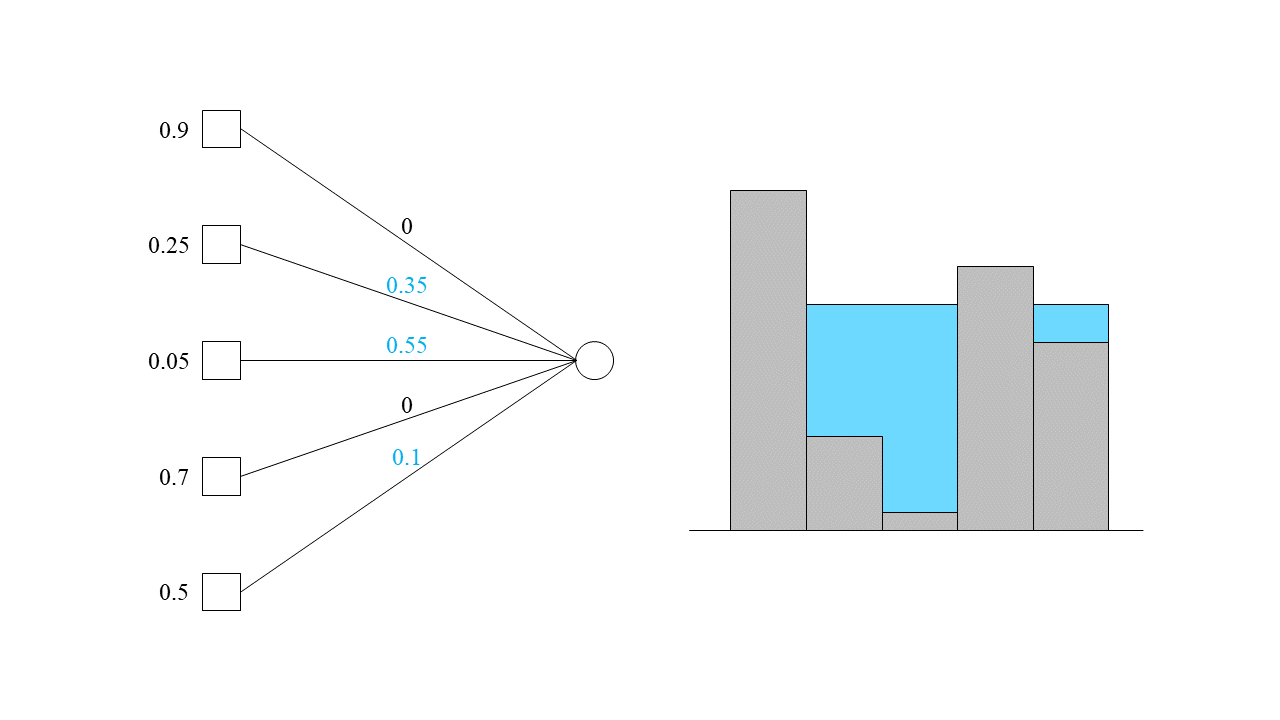
이렇게 작업을 할당해 준다면 우리가 원하는 대로 인접한 모든 기계에 동일한 부하를 줄 수 있게 됩니다. 물론 몇몇 기계에는 더 많은 부하가 실려있을 수 있습니다. 하지만 이는 이번 작업이 들어오기 전부터 이미 높은 부하를 가졌을 때뿐입니다. 그러한 기계에다가는 작업을 할당하지 않습니다.
고려하지 않은 경우가 하나 있습니다. 각 기계는 합해서 최대 1의 작업량을 할당 받을 수 있습니다. 따라서 작업을 넣는 작업을 진행하기 전에 인접한 기계들이 모두 부하가 높은 상황이라면, 작업을 인접한 기계에 모두 할당해 주지 못할 수 있습니다. 기존의 결정을 번복할 수 없으므로 인접한 기계가 모두 1의 부하를 받는 때가 오면, 남은 작업 조각들은 버리는 수밖에 없습니다.
이러한 방식으로 동작하는 알고리즘을 물 채우기 알고리즘(water-filling algorithm)이라고 부릅니다. 알고리즘이 동작하는 것을 보면 그러한 이름이 붙은 것이 직관적으로 다가올 것입니다. 새로운 작업이 도착했을 때, 각 인접한 기계들마다 할당받을 수 있는 여유분을 깊이로 하는 통에다가 용량이 1인 물을 붓는 것으로 생각할 수 있기 때문입니다. 들어간 물은 평평한 수면을 이룰 것이므로 종국적으로 인접한 기계들은 동일한 부하를 받게 될 것입니다. 만약 통의 깊이가 얕다면 모든 물을 부을 수 없을 것이고, 이때는 남은 물을 버려야 하겠습니다.
위 내용을 정형화하면 아래와 같이 적을 수 있습니다. 여기서 \((a)_+ := \max\{ a, 0 \}\)을 의미합니다.
알고리즘 1. 물 채우기 알고리즘
초기 입력: 기계 \(L\)
출력: 할당 \(\{x_e\}_{e \in E}\)
- 매 시각 작업 \(j \in R\)가 도착하면 아래를 수행한다.
- 인접한 기계 \(i \in N(j)\)에 대해, 현재까지 \(i\)가 할당 받은 작업량을 \(d_i := \sum_{e \in \delta(i)} x_e\)라고 한다.
- \(\sum_{i \in N(j)} ( \ell(j) - d_i )_+ = 1\)이 되도록 하는 \(\ell(j)\)을 찾는다.
- \( \bar{\ell}(j) \gets \min \{\ell(j), 1\} \).
- 인접한 기계 \(i \in N(j)\)에 대해, \(x_{(i, j)} \gets (\bar{\ell}(j) - d_i)_+\).
알고리즘 분석
이제 알고리즘을 분석해 보도록 하겠습니다. 아래의 논의는 이전 글을 참고하시면 이해하기 쉽습니다.
온라인 이분 매칭 랭킹 알고리즘 (Ranking Algorithm for Online Bipartite Matching)
지난번에 온라인 이분 매칭 문제(online bipartite matching problem)에 대해서 알아 보았습니다. 그 문제는 다음과 같이 정의되었습니다. 처음에는 가용할 수 있는 택시 몇 대가 주어진다. 이후 시간이 흐
gazelle-and-cs.tistory.com
앞에서 우리는 알고리즘의 출력 \(x\)가 결국은 아래 LP의 가능한 해(feasible solution)라고 했습니다.
\[ \begin{array}{rll} \text{maximize } & \displaystyle \sum_{e \in E} x_e \\ \text{subject to } & \displaystyle \sum_{e \in \delta(i)} x_e \leq 1, & \forall i \in L, \\ & \displaystyle \sum_{e \in \delta(j)} x_e \leq 1, & \forall j \in R, \\ & x_e \geq 0, & \forall e \in E. \end{array} \tag{P} \]
이 LP의 쌍대는 아래와 같습니다.
\[ \begin{array}{rll} \text{minimize } & \displaystyle \sum_{i \in L} \alpha_i + \sum_{j \in R} \beta_j \\ \text{subject to } & \alpha_i + \beta_j \geq 1, & \forall (i, j) \in E, \\ & \alpha_i, \beta_j \geq 0, & \forall i \in L, \forall j \in R. \end{array} \tag{D} \]
두 LP는 다음의 유용한 성질을 갖습니다.
정리 1. LP 쌍대성
LP (P)에 가능한 임의의 해 \(x^*\)와 LP (D)에 가능한 임의의 해 \( (\alpha, \beta) \)에 대해, 항상 \[ \sum_{e \in E} x^*_e \leq \sum_{i \in L} \alpha_i + \sum_{j \in R} \beta_j \]를 만족한다.
따라서 만약 우리가 \[ \sum_{e \in E} x_e \geq \gamma \left( \sum_{i \in L} \alpha_i + \sum_{j \in R} \beta_j \right) \]를 만족하는 LP (D)에 가능한 해 \((\alpha, \beta)\)를 찾는다면, 이 알고리즘이 \(\gamma\)-경쟁 알고리즘이 된다는 것을 보일 수 있게 됩니다.
그러한 \((\alpha, \beta)\)를 만드는 방법을 바로 설명할 수도 있겠지만, 그러면 직관적으로 이해하기 어렵다고 생각합니다. 저 또한 원래 증명을 머리로는 알고 있었습니다만, 마음으로는 받아들이지 못하는 상황이었습니다. 최근 관련 주제로 연구를 하면서 다시 공부할 일이 있었는데, 이번에 증명을 나름 직관적으로 이해하는 좋은 방법을 찾았습니다. 이 글을 작성하게 된 계기도 이 증명을 기록하고 싶었기 때문입니다.
쌍대 문제 (D)에 가능한 해는 직관적으로 무엇에 해당할까요? 한번 \((\alpha, \beta)\)의 모든 값이 0 또는 1만을 갖는다고 가정해 봅시다. 정점들 중에서 \(\alpha_i = 1\)인 \(i\)와 \(\beta_j = 1\)인 \(j\)를 모아서 \(S\)라고 부르겠습니다. LP (D)의 제약 조건에 의해서 우리는 각 간선 \((i, j) \in E\)에 대해 \(\alpha_i = 1\)이거나 \(\beta_j = 1\)이라는 사실을 알 수 있습니다. 다시 말해 \(i\)와 \(j\) 중 적어도 하나는 \(S\)에 속해야 한다는 뜻입니다. 이러한 조건을 만족하는 \(S\)를 우리는 특별한 이름으로 부릅니다. 바로 정점 덮개(vertex cover)입니다. 즉 LP (D)는 정점 덮개의 선형 계획법 완화에 해당합니다.
이분 매칭의 쌍대 문제가 정점 덮개를 표현한다는 사실은 그다지 놀라운 일이 아닙니다. 둘 사이의 연관성은 다음의 유명한 정리에서 확연히 드러납니다.
정리 2. 쾨니그의 정리
어떤 이분 그래프가 주어졌을 때, 이분 그래프의 최대 매칭의 크기는 최소 정점 덮개의 크기와 동일하다.
위 정리가 궁금하신 분들은 아래의 글을 참고하시기 바랍니다.
쾨니그의 정리 (Kőnig's Theorem)
이 글은 홀의 정리 (Hall's Theorem)와 밀접한 연관이 있습니다. 필요한 경우에는 이를 참조하세요.2019/01/28 - [조합론적 최적화] - 홀의 정리 (Hall's Theorem) 무언가를 최적화시키는 문제를 보면 생각보
gazelle-and-cs.tistory.com
쾨니그의 정리를 통해 우리는 이분 그래프 \(G = (L \cup R, E)\)의 최소 정점 덮개 \(S\)가 다음 성질들을 만족한다는 것을 알 수 있습니다.
- \(L\)과 \(R\)은 각각 \(L \cap S\), \(L \setminus S\)와 \(R \cap S\)와 \(R \setminus S\)로 분할(partition)된다.
- \(L \setminus S\)와 \(R \setminus S\)에는 간선이 존재하지 않는다.
- \(L \cap S\)의 모든 정점이 \(R \setminus S\)의 정점과 짝지어지는 매칭이 존재한다.
- \(R \cap S\)의 모든 정점이 \(L \setminus S\)의 정점과 짝지어지는 매칭이 존재한다.
각 조건을 만족하는 이유를 논의해 보겠습니다. 먼저, 만약 \(L \setminus S\)와 \(R \setminus S\)에 간선이 존재한다면, \(S\)는 정점 덮개조차 아니게 되므로 두 번째 조건은 성립해야 합니다. 세 번째와 네 번째 조건은 최대 매칭의 크기와 동일해야 하므로 만족합니다. 예를 들어 어떤 매칭이 \(L \cap S\)의 한 정점과 \(R \cap S\)의 한 정점을 짝지어 준다고 해 봅시다. 그러면 그 매칭의 크기는 죽었다 깨어나도 \(|S|\)가 될 수 없습니다. 따라서, 크기가 반드시 \(|S|\)여야 하는 최대 매칭에서는 \(L \cap S\)의 정점들은 \(R \setminus S\)의 정점들과, \(R \cap S\)의 정점들은 \(L \setminus S\)의 정점들과만 짝지어져야 합니다. 그 크기가 정확히 \(|S|\)이려면 \(L \cap S\)와 \(R \cap S\)의 모든 정점들이 짝지어져야 합니다.
각설하고, 우리의 목표가 무엇이었는지 다시 생각해 보겠습니다. 우리의 목표는 알고리즘의 출력 \(x\)에 대해, \[ \sum_{e \in E} x_e \geq \gamma \left( \sum_{i \in L} \alpha_i + \sum_{j \in R} \beta_j \right) \tag{1} \]를 만족하는 LP (D)에 가능한 해 \((\alpha, \beta)\)를 찾는 것입니다. 그러기 위해서는 가능한 \(\sum_{i \in L} \alpha_i + \sum_{j \in R} \beta_j\)의 값이 작아야 하겠습니다. 만약 최종 입력 그래프에 대한 최소 정점 덮개 \(S\)를 안다면, \[ \alpha_i := \begin{cases} 1, & i \in L \cap S \\ 0, & i \in L \setminus S, \end{cases} \quad \beta_j := \begin{cases} 1, & j \in R \cap S, \\ 0, & j \in R \setminus S \end{cases} \]를 해 주는 것으로 좋은 쌍대 해를 얻을 수 있습니다.(사실은 최적해입니다.)
문제는 알고리즘이 동작하는 도중에는 전체 입력이 어떻게 될지 모르므로 \(S\)를 알 수 없다는 데에 있습니다. 대신 각 기계 혹은 작업의 상태에 따라 어렴풋이 유추해 볼 수는 있겠습니다. 먼저 기계의 입장에서 생각해 보겠습니다. 알고리즘이 거의 끝나는 와중에 해당 기계에 할당된 부하가 크다면 아무래도 \(S\)에 속할 것으로 예측할 수 있습니다. 최대 매칭에서 \(L \cap S\)의 모든 정점은 짝지어져야 하기 때문이죠. 반대로 부하가 작은 기계는 \(S\)에 속할 가능성이 낮을 것입니다.
이번에는 작업의 경우를 생각해 봅시다. 어떤 작업을 처리한 후에 인접한 작업들의 부하가 작다면, 이 작업은 \(S\)에 속할 공산이 큽니다. 앞에서 인접한 기계들의 부하가 작다면 \(L \setminus S\)에 들어갈 가능성이 높다고 했는데, 해당 기계들은 \(R \cap S\)의 작업에만 인접할 수 있기 때문입니다. 반대로 인접한 기계들의 부하가 크다면, 해당 기계들이 \(L \cap S\)에 속할 가능성이 높으므로 이 작업은 \(S\)에 속하지 않을 것을 예상할 수 있겠습니다.
정리하자면 다음과 같습니다.
- 각 기계 \(i \in L\)는 그것에 할당된 부하가 클수록 \(S\)에 들어갈 것이다.
- 각 작업 \(j \in R\)는 이 작업을 처리한 후 인접한 기계들의 부하가 크지 않다면 \(S\)에 들어갈 것이다.
기계에 할당된 부하는 \(d_i := \sum_{e \in \delta(i)} x_e\)와 같습니다. 따라서 \(S\)에 \(i\)가 들어갈지 여부는 \(d_i\)로 결정해도 괜찮을 것입니다. 그렇다면 각 작업 \(j\)가 \(S\)에 들어가는지 여부를 나타내는 적절한 척도는 무엇일까요? 바로 \(\bar{\ell}(j)\)입니다. 이 값은 작업 \(j\)를 처리한 후 인접한 기계 중 \(j\)의 작업이 조금이라도 할당된 기계들의 부하 값이므로, \(\bar{\ell}(j)\)의 값이 작을 때 \(S\)에 \(j\)가 들어간다고 해석하는 것이 직관적으로 그리 무리는 아닐 것입니다.
\(f(0) = 0\), \(f(1) = 1\)을 만족하는 미분 가능한 증가 함수 \(f\)를 하나 생각해 보겠습니다. 그리고 각 기계 \(i \in L\)에 대해서는 매번 \( \alpha_i \gets f(d_i) \)를 갖도록 하고, 각 작업 \(j \in R\)에 대해서는 \( \beta_j \gets 1 - f(\bar{\ell}(j))\)의 값을 갖도록 해 보겠습니다. 참고로 \(\alpha_i\)는 알고리즘이 진행됨에 따라 변화할 수 있으나, \(\beta_j\)는 작업 \(j\)가 처리된 후에는 고정된 값을 갖습니다. 이러면 \( (\alpha, \beta) \)가 앞에서 논의한 사항을 잘 반영한다는 것을 확인할 수 있습니다.
이렇게 정의된 \((\alpha, \beta)\)는 우리가 원하는 목표의 절반을 이루어 줍니다.
정리 3. 가능한 쌍대 해
\((\alpha, \beta)\)는 쌍대 문제 (D)에 가능한 해이다.
[증명] \(\alpha, \beta \geq 0\)은 자명합니다. 각 간선 \((i, j) \in E\)에 대해, \(j\)가 처리된 후 기계 \(i\)의 부하는 적어도 \(\bar{\ell}(j)\)이고, 이후 줄지 않습니다. 따라서 \(d_i \geq \bar{\ell}(j)\)를 만족하고, \[ \alpha_i + \beta_j = f(d_i) + 1 - f(\bar{\ell}(j)) \geq f(\bar{\ell}(j)) + 1 - f(\bar{\ell}(j)) = 1 \]이 성립합니다. ■
남은 것은 식 (1)을 만족하는 적절한 \(\gamma\)를 찾는 것입니다.
정리 4. 알고리즘의 경쟁성
알고리즘의 출력 \(x\)와 함수 \(f\)에 의해 만들어진 쌍대 해 \( (\alpha, \beta) \)는 \[ \gamma = \frac{1}{\max_{t \in [0, 1]} \{ 1 - f(t) + f'(t) \} } \]에 대해 식 (1)을 만족한다.
[증명] 편의를 위해 \[ P := \sum_{e \in E} x_e, \quad D := \sum_{i \in L} \alpha_i + \sum_{j \in R} \beta_j, \quad \Gamma := \max_{t \in [0, 1]} \{ 1 - f(t) + f'(t) \} \]라고 쓰겠습니다. 이제 알고리즘이 시작할 때를 고려해 봅시다. 아직까지 할당한 것이 하나도 없으므로 \(P = 0\)입니다. 또한, \(f(0) = 0\)이라고 하였으므로, \(Q=0\)을 만족합니다. 따라서 만약 매 작업 \(j\)에 대해, 이 작업을 처리한 후 \(P\)와 \(D\)의 변화량 \(\mathit{\Delta} P\)와 \(\mathit{\Delta} Q\)가 \[ \Gamma \mathit{\Delta} P \geq \mathit{\Delta} Q \]를 만족함을 보인다면 증명이 완성됩니다.
각 \(i \in N(j)\)에 대해, \(d_i\)는 이번 작업을 처리하기 직전 각 \(i\)가 그동안 받은 할당량이라고 하겠습니다. 이제 임의의 \(t \in [0, 1]\)에 대해, \(n(t)\)를 \(t\)보다 적은 양을 할당 받은 기계의 대수라고 하겠습니다. 즉, \[ n(t) := |\{i \in N(j) \mid d_i \leq t\}| \]입니다. 이전 절에서 활용한 예시에 대해 도식적으로 나타내면 아래와 같습니다.
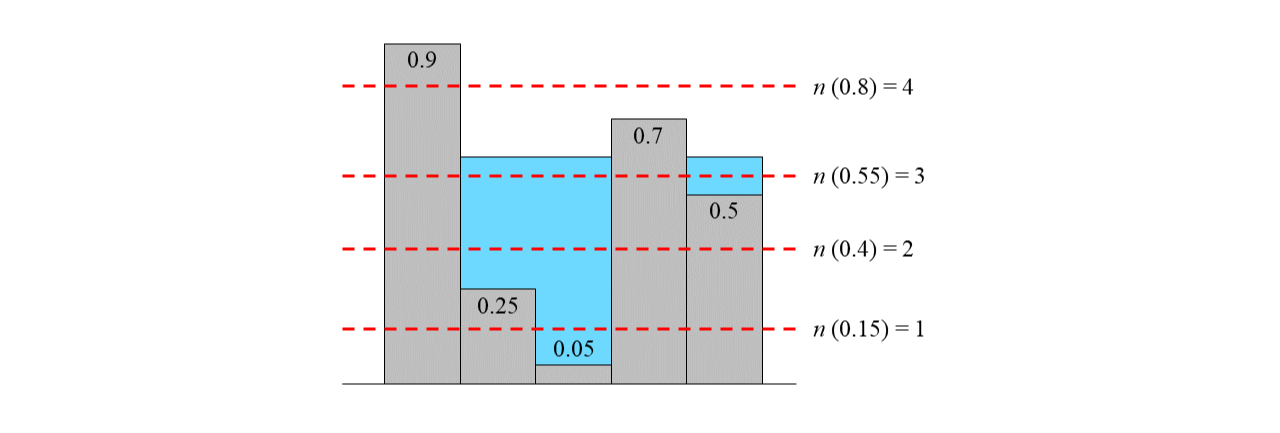
직관적으로 설명하면, \(t\)는 일종의 "수심(水深)"에 해당하고, \(n(t)\)는 수심이 \(t\)보다 "낮은" 기계들의 대수를 의미합니다.
이 정의를 활용하면 \(\mathit{\Delta} P\)와 \(\mathit{\Delta} Q\)를 각각 수심 \(t\)에 대한 식으로 표현할 수 있습니다. 먼저, \[ \mathit{\Delta} P = \sum_{e \in \delta(j) } x_e = \int_0^{\bar{\ell}(j)} n(t) dt \]가 성립함을 확인하시기 바랍니다. 알고리즘의 동작을 수심이 \(t\)가 되었을 때 \(d_i \leq t\)인 기계 \(i \in N(j)\)에 동일한 속도로 작업을 할당하는 것으로 볼 수 있기 때문입니다.
이제 \(\mathit{\Delta} Q\)를 생각해 보겠습니다. 이는 \(\alpha\)가 증가한 양과 \(\beta\)가 증가한 양으로 나눌 수 있습니다. 각 기계 \(i \in N(j)\)의 부하는 \(d_i\)에서 \(\max\{\bar{\ell}(j), d_i\}\)로 바뀌었습니다. 따라서, \[ \mathit{\Delta} \alpha_i = f(\max \{ \bar{\ell}(j), d_i \}) - f(d_i) = \int_{d_i}^{\max\{ \bar{\ell}(j), d_i \}} f'(t) dt \]로 쓸 수 있습니다. 이를 모두 더하면, \[ \sum_{i \in N(j)} \mathit{\Delta} \alpha_i = \int_0^{\bar{\ell}(j)} f'(t) n(t) dt \]와 동일합니다.
마지막으로 \(\beta\)의 증가량은 \(\beta_j\)의 값이 \(1 - f(\bar{\ell}(j))\)로 바뀌는 것과 같습니다. 만약 \(\bar{\ell}(j) = 1\)이라면 \(f\)가 \(f(1) = 1\)을 만족하는 증가함수라는 조건에 의해 \[\beta_j = 0 \leq \int_0^{\bar{\ell}(j)} (1 - f(t)) n(t) dt \]임을 알 수 있습니다. 반면, \(\bar{\ell}(j) = \ell(j)\)라면, 작업 \(j\)는 1의 작업량을 모두 할당했다는 의미이므로 \( \int_0^{\ell(j)} n(t) dt = 1 \)이 되며, 따라서 \[ 1 - f(\ell(j)) = (1 - f(\ell(j))) \int_0^{\ell(j)} n(t) dt \leq \int_0^{\ell(j)} (1 - f(t)) n(t) dt \]를 유도할 수 있습니다.
이를 모두 조합하면, \[ \mathit{\Delta} Q \leq \int_0^{\bar{\ell}(j)} (f'(t) + 1 - f(t)) n(t) dt \leq \Gamma \int_0^{\bar{\ell}(j)} n(t) dt = \Gamma \mathit{\Delta} P \]를 이끌어 낼 수 있습니다. ■
이제 남은 것은 적절한 \(f\)를 결정하는 일입니다. 찾고 싶은 \(f\)의 조건을 다시 적어 보자면 아래와 같습니다.
- \(f\)는 미분 가능한 증가함수이다.
- \(f(0) = 0\), \(f(1) = 1\)을 만족한다.
- \( \Gamma = \max_{t \in [0, 1]} \{ 1 - f(t) + f'(t) \} \)를 최소화한다.
\(f(t) := \frac{e^t - 1}{e - 1}\)로 정의하면 위 조건을 모두 만족하면서 \( \Gamma = \frac{e}{e - 1} \)이 됨을 보일 수 있습니다. 따라서 알고리즘의 경쟁비는 \(\gamma = 1/\Gamma = 1 - 1/e\)가 됩니다.
마치며
이것으로 온라인 분수 이분 매칭 문제에 대한 설명을 마칩니다. 특히, 본문에서는 이 문제를 \(1-1/e\)의 경쟁비로 해결하는 결정론적 알고리즘인 물 채우기 알고리즘에 대해 깊이 다루었습니다. 이제 궁금한 점은 분명 더 좋은 경쟁비를 가질 수 있는지입니다. 정수 문제에서 처럼 랜덤 알고리즘을 사용하면 혹여나 더 좋은 경쟁비를 가질 수도 있겠습니다. 하지만 안타깝게도, 이 문제는 더 이상, 심지어 랜덤 알고리즘이라 할지라도 더 좋은 경쟁비로 해결할 수 없습니다. 다음 시간에는 이에 대해 알아 보도록 하겠습니다.
고맙습니다. :)
참고자료
[1] Bobby Kleinberg. Lecture note of CS 6820 Analysis of Algorithms, Cornell University, Fall 2012. [Link]
'온라인 알고리즘 > Online matching' 카테고리의 다른 글
| 온라인 이분 매칭 경쟁비 상한 (Upper Bound of Competitive Ratio for Online Bipartite Matching) (0) | 2024.03.12 |
|---|---|
| 온라인 메트릭 이분 매칭 (Online Metric Bipartite Matching) (0) | 2022.02.26 |
| 온라인 가중치 이분 매칭 (Online Weighted Bipartite Matching) (0) | 2021.02.14 |
| 온라인 이분 매칭 랭킹 알고리즘 (Ranking Algorithm for Online Bipartite Matching) (0) | 2021.01.09 |
| 온라인 이분 매칭 (Online Bipartite Matching) (0) | 2020.11.07 |
