
최단 경로 문제(shortest path problem)는 가장 유명한 조합론적 최적화 문제 중 하나로, 이름에서 유추할 수 있듯이 다양한 분야에서 널리 활용되는 문제입니다. 지난 포스트에서는 이 문제를 정확히 정의하고 최단 경로가 갖는 구조적인 특징을 이해하였으며, 마지막으로 \( O(|V||E|) \) 시간에 이를 해결하는 벨만-포드 알고리즘(Bellman-Ford algorithm)에 대해서도 공부했습니다.
최단 경로 문제 & 벨만-포드 알고리즘 (Shortest Path Problem & Bellman-Ford Algorithm)
자동차를 타고 서울에서 부산까지 여행을 떠난다고 생각해 봅시다. 일분일초라도 여행을 더 즐기기 위해서는 빨리 목적지에 도달하는 것이 좋겠죠. 그러려면 어떤 경로를 따라 자동차를 운전해
gazelle-and-cs.tistory.com
컴퓨터과학을 공부하다 보면 항상 맞닥뜨리는 질문이 있지요. 과연 더 잘할 수 있을까요? 놀랍게도, 만약 간선의 모든 "비용"이 음이 아니라면 정점의 제곱 시간에 가능합니다. 그 방법이 바로 다익스트라의 알고리즘(Dijkstra's algorithm)인데요. 이번 시간에는 이에 대해서 함께 알아 보도록 하겠습니다.
복습
지난 포스트에서 공부한 내용을 정리해 보겠습니다. 먼저 최단 경로 문제의 정의는 다음과 같았습니다. 문제의 입력으로 우리에게는 방향이 있는 그래프(directed graph) \(G = (V, E)\)와 간선의 비용 \(c: E \to \mathbb{Q}_+\), 그리고 출발지 \(s \in V\)가 주어집니다. 이때 이번에는 간선의 비용이 항상 음이 아니라고 가정하겠습니다. 우리의 목표는 모든 정점 \(v \in V\)에 대해, \(s\)에서 출발하여 \(v\)에 도달하는 경로 중에서 가장 비용이 저렴한 것, 즉 최단 경로를 찾는 것입니다.
입력 그래프에 음의 비용을 갖는 순환이 없다면 최단 경로에 순환이 없다고 가정할 수 있고, 출발지를 제외한 모든 정점마다 최단 경로 상 직전에 위치한 정점이 무엇인지를 찾는 것으로 최단 경로 문제를 해결할 수 있다고 하였습니다. 이는 최단 경로 트리(shortest path tree)라는 특별한 트리 구조의 형태로 표현되었죠. 다음 정리는 이를 보이는 데 유용한 정리 중 하나였습니다.
정리 1. 최단 경로들의 관계
임의의 방향 그래프 \(G = (V, E)\)와 간선 비용 \(c : E \to \mathbb{Q}\) 그리고 출발지 \(s \in V\)가 주어졌다고 하자. 임의의 정점 \(v \in V\)에 대해, \( P = \langle s, \cdots, u, v \rangle \)가 \(s\)에서 \(v\)로 향하는 최단 경로라고 하자. 그러면 \(P\)에서 마지막 \(v\)를 제거한 경로 \(P'\)은 \(s\)에서 \(u\)까지 향하는 최단 경로이다.
이번 포스트에서는 음이 아닌 비용만을 고려하므로 입력 그래프에 음의 비용을 갖는 순환이 없다는 것은 자명합니다. 따라서 위 정리를 포함해 이전 포스트에서 배운 내용들도 모두 그대로 성립합니다.
직관적으로 이해하기
음이 아닌 비용을 갖는 그래프에는 도대체 어떤 다른 성질이 있길래 더 빠른 알고리즘을 만들 수 있는 것일까요? 아래 예시를 함께 살펴 보겠습니다.
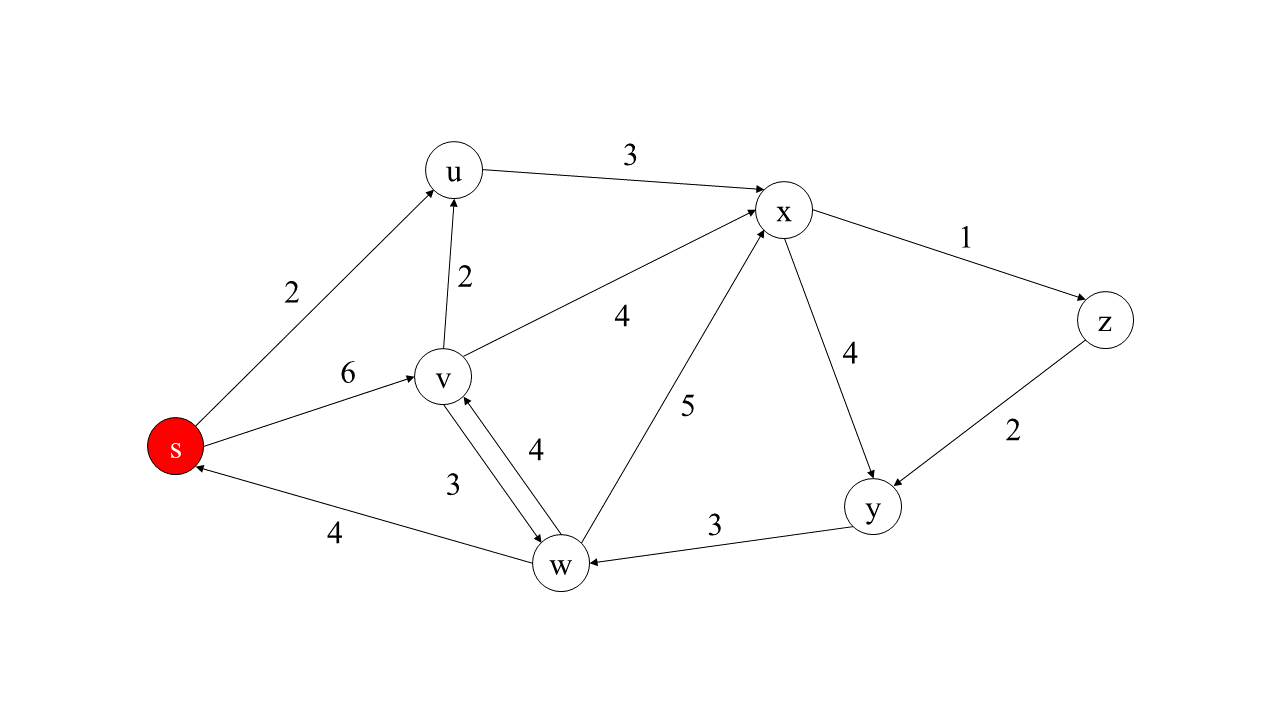
\(s\)는 출발지이므로 자명하게 0의 비용을 가질 것입니다. 우리의 목표는 모든 정점에 대해 \(s\)에서 출발하여 해당 정점에 도달하는 최단 경로를 구하는 것입니다. 따라서 분명 해당 경로는 \(s\)에 인접한(adjacent) 정점인 \(u\) 혹은 \(v\)를 반드시 지날 것입니다. 따라서 \(u\)와 \(v\)에 대해서 고려해 보도록 합시다.
우리는 2의 비용으로 \(u\)에, 6의 비용으로 \(v\)에 도달할 수 있습니다. 여기서 우리는 한 가지 흥미로운 사실을 발견할 수 있는데요. 바로, \(s\)에서 \(u\)로 가는 비용은 2가 최선이라는 것입니다. 왜 그럴까요? \(s\)에서 바로 \(u\)로 가지 않으면서 \(u\)에 도달하려면 분명 \(s\)에서 \(v\)로 가야 합니다. 문제는 \(s\)에서 바로 \(v\)로 향하면 6의 비용을 지불해야 한다는 점이죠. 간선의 모든 비용은 항상 음이 아니라고 하였으므로 \(s\)에서 \(v\)를 경유하여 \(u\)로 향하는 경로의 비용은 6보다 작을 수 없습니다. 따라서 \(s\)에서 \(u\)로 바로 가는 것이 최선의 방법임을 알 수 있죠.
그럼 반대로 \(s\)에서 \(v\)로 바로 향하는 것은 최단 경로를 이룰까요? \(s\), \(u\), \(v\)만 고려한 상황에서는 이를 장담할 수 없습니다. \(s\)에서 \(v\)로 바로 향하지 않고 \(u\)를 거친 다음에 \(v\)에 도달하는 것이 더 저렴할 수 있기 때문이죠.

\(u\)의 최단 경로가 정해졌으니 그림 2에서와 같이 고정시켜 보겠습니다. 다음으로는 고정된 정점들에 인접한 정점들을 생각해 봅시다. \(s\)에서 아직 고정되지 않은 정점으로 향하는 최단 경로는 분명 현재 고정된 정점들에 인접한 정점들 중 하나를 지날 것이기 때문이죠. 후보는 \(v\)와 \(x\)가 있습니다. \(v\)는 \(s\)에 6의 비용으로 인접해 있고, \(x\)는 \(u\)에 3의 비용으로 인접해 있습니다.
우리는 여기서 또 둘 중 하나의 최단 경로를 결정할 수 있는데요. 바로 \(x\)입니다. \(s\)에서 \(u\)까지 최단 경로로 와서 \(x\)로 가는 경로는 5의 비용을 갖습니다. 하지만 간선 \( \langle u, x \rangle \)를 통하지 않고 \(x\)에 도달하기 위해서는 분명 \( \langle s, v \rangle \)를 타야 합니다. 이는 이미 6의 비용을 발생시키므로 이를 통해서는 절대로 최단 경로를 얻을 수 없습니다.

이렇게 매번 최단 경로가 결정된 정점들에 인접한 정점들 중에서 가장 저렴한 비용으로 도달할 수 있는 정점을 하나 골라서 이것의 최단 경로를 결정하는 방식으로 진행한다면 아마도 모든 정점에 대한 최단 경로를 구하게 된다는 것을 예상할 수 있습니다.
그렇다면, 음의 비용을 갖는 간선이 있을 때는 도대체 무슨 문제가 있길래 위 방법이 성립하지 않는 것일까요? 다음 그림을 잘 생각해 보면 쉽게 답을 알 수 있습니다.

위 그림에서 \(s\)만 고정된 상태일 때, \(u\)와 \(v\) 중 \(u\)로 바로 가는 것이 최단 경로처럼 보입니다. 아무래도 \(s\)에서 \(v\)로 가는 건 100의 비용을 내야하지만 \(u\)로 가는 것은 2의 비용만 내니 말이죠. 하지만 실제로는 \(v\)를 거쳐서 \(u\)로 가는 것이 이득입니다. 즉, 현재까지 고정된 정점들에서 인접한 정점들 중 어떤 정점이 최단 경로가 고정될지 알 수 없으므로 위 방법은 더 이상 성립하지 않습니다.
우선순위 큐(Priority Queue)
이전 절에서 고안한 알고리즘은 최단 경로가 고정된 정점들을 유지하면서 매번 그것들에 인접한 정점들 중 가장 적은 비용으로 도달할 수 있는 정점을 새로이 고정시켜주는 방식으로 동작했습니다. 이를 실제로 구현하기 위해서는 매번 고정되지 않은 정점들마다 얼마큼의 비용으로 \(s\)로부터 도달할 수 있는지 기록해 놓으면서 그중 가장 저렴한 정점을 빠르게 찾을 수 있어야 합니다.
이 작업을 도와주는 자료 구조가 있습니다. 바로 우선순위 큐(priority queue)입니다. 이 자료 구조는 자료를 저장할 때 키(key)를 함께 저장했다가 키가 가장 작은 순서대로 자료를 반출하는 구조로, 다음과 같은 동작을 수행합니다.
- \(\mathsf{enqueue}(v, k)\): \(k\)의 키를 갖는 자료 \(v\)를 저장한다.
- \(\mathsf{decreasekey}(v, k')\): \(v\)의 키를 \(k'\)으로 낮춘다. (\(v\)가 저장되어 있고 키가 작아지는 경우만 생각한다.)
- \(\mathsf{dequeue}()\): 현재 저장된 자료들 중에서 키가 가장 작은 자료를 반출한다.
우선순위 큐에 1부터 \(n\)까지 총 \(n\) 개의 자료를 저장할 예정이라고 합시다. 사실 우선순위 큐는 이보다 훨씬 일반적인 경우에도 동작할 수 있는 자료 구조이나, 본문에서는 해당 경우만 고려할 예정이므로 충분합니다. 대신 키는 별다른 조건이 없습니다. 우선순위 큐를 어떻게 구현할 수 있을까요?
가장 간단한 구현 방식은 길이가 \(n\)인 배열 \(a\)를 만들고 \(a[i]\)에는 자료 \(i\)의 키를 저장하는 것입니다. (인덱스는 1부터 시작한다고 합시다.) 자세히 말하면, 먼저 모든 \(i\)에 대해 \( a[i] \gets \mathsf{nil} \)로 설정한 다음, 위 동작들은 다음과 같이 구현하는 것이죠. 여기서 \( \mathsf{nil} \)의 의미는 해당 자료가 우선순위 큐에 들어와 있지 않다는 의미입니다.
- \(\mathsf{enqueue}(v, k)\): \( a[v] \gets k \)를 수행한다.
- \(\mathsf{decreasekey}(v, k')\): \( a[v] \gets k' \)을 수행한다.
- \(\mathsf{dequeue}() \): \(a\)를 차례대로 훑어서 가장 키가 작은 \(v^*\)를 찾고 \(a[v^*] \gets \mathsf{nil}\)을 수행한다. 이후 \(v^*\)를 반환한다.
우선순위 큐를 이렇게 구현하게 되면 \(\mathsf{enqueue}\)와 \(\mathsf{decreasekey}\)는 \(O(1)\), 마지막으로 \(\mathsf{dequeue}\)는 \( O(n) \)의 시간이 소요됨을 쉽게 알 수 있습니다.
이외에도 우선순위 큐를 구현하는 여러 방법이 존재합니다. 하지만 이를 모두 소개하기에는 내용이 너무 방대하므로 대표적인 두 가지 구현인 이진 힙(binary heap)과 피보나치 힙(Fibonacci heap)에 대한 위 동작들의 수행 시간을 밝히는 것으로 대신합니다. 나중에 기회가 되면 다루어 보도록 하겠습니다. 특히 피보나치 힙은 재미있는 내용이 많아서 언젠가 꼭 다루었으면 합니다.
| 본문의 쉬운 구현 | 이진 힙 | 피보나치 힙 | |
| \(\mathsf{enqueue}\) | \(O(1)\) | \(O(\log n)\) | \(O(1)\) |
| \(\mathsf{decreasekey}\) | \(O(1)\) | \(O(\log n) \) | \(O(1)^*\) |
| \(\mathsf{dequeue}\) | \(O(n)\) | \(O(\log n) \) | \(O(\log n)^*\) |
위 표에서 *은 분할 상환 기법(amortized analysis)으로 분석한 수치입니다. 분할 상환 기법에 대한 내용은 다른 글에서 다루었으니 궁금하시면 참고하시기 바랍니다.
2021.04.08 - [알고리즘 기초/Algorithm design] - 분할 상환 분석 (Amortized Analysis)
분할 상환 분석 (Amortized Analysis)
이번 포스트에서는 분할 상환 분석(amortized analysis)에 대해서 알아보도록 하겠습니다. 자료 구조나 알고리즘 수업을 들으셨다면 분명 한 번쯤은 들어 보신 개념일 것입니다. 개인적으로는 자료
gazelle-and-cs.tistory.com
알고리즘 및 분석
이전 절에서 고찰한 내용을 토대로 알고리즘을 작성하면 다음과 같습니다. 아래 알고리즘이 바로 이번 포스트의 주제인 다익스트라의 알고리즘입니다.
알고리즘 1. Dijkstra's algorithm
입력: 방향이 있는 그래프 \(G = (V, E)\), 간선 비용 \(c : E \to \mathbb{Q}_+\), 출발지 \(s \in V\)
출력: 최단 경로 트리
- 정점을 \(1, \cdots, |V|\)라고 하고, \(Q\)를 이 정점들을 저장할 예정인 우선순위 큐라고 하자.
- \(d[s] \gets 0 \text{ & } d[v] \gets \infty, \forall v \in V \setminus \{s\}\)
- \(S \gets \emptyset\)
- \(Q.\mathsf{enqueue}(s, 0)\)
- \(Q\)에 저장된 정점이 없을 때까지 아래를 반복한다.
- \( u \gets Q.\mathsf{dequeue}() \)
- \( S \gets S \cup \{ u \}\)
- \(u\)에서 나가는 방향으로 인접한 모든 정점 \(v\) 중 \( d[v] > d[u] + c(u, v) \)를 만족하면 아래를 수행한다.
- \(d[v] \gets d[u] + c(u,v)\)
- \(\pi(v) \gets u\)
- 만약 \(d[v] = \infty\)였다면, \( Q.\mathsf{enqueue}(v, d[u] + c(u,v)) \); 그렇지 않았다면, \( Q.\mathsf{decreasekey}(v, d[u] + c(u, v)) \)
- \( \{ \langle \pi(v), v \rangle : v \in S \setminus \{s\} \} \)를 반환한다.
이제 이 알고리즘이 실지로 올바른 답을 출력하는지를 따져 봅시다. 사실 「직관적으로 이해하기」 절에서 개괄적인 증명의 방식을 살펴 보았습니다. 아래는 이를 수학적으로 엄밀하게 밝혀 적은 것입니다.
먼저 \(S\)가 실제로 \(s\)에서 도달 가능한 정점들로만 이루어져 있는지를 따져 보아야 합니다. 다시 말해서, 엉뚱하게 \(s\)에서 도달 가능하지 않은데 \(S\)에 들어가 있는 경우나, 반대로 \(s\)에서 도달 가능한데 \(S\)에 들어있지 않은 경우가 존재하지 않는다는 것을 보여야 하지요. 그래야 알고리즘 1이 출력하는 것을 믿을 수 있습니다.
정리 2. \(S\)의 도달 가능성
알고리즘 1이 모두 끝난 후 \(S\)는 \(s\)에서 도달 가능한 정점들로만 이루어져 있다.
[증명] 먼저 \(S\)의 모든 정점들이 \(s\)에서 도달 가능한지를 따져 봅시다. 어떤 정점이 \(S\)에 들어 있으려면 언젠가 우선순위 큐 \(Q\)에 \(\mathsf{enqueue}\)가 되어야 합니다. 언제 \(\mathsf{enqueue}\)가 되는지를 따져보면 이전에 \(\mathsf{enqueue}\)가 된 정점들로부터 인접할 때입니다. \(Q\)는 맨 처음에 \(s\)가 \(\mathsf{enqueue}\)된 상태로 시작하며, \(s\)는 당연히 \(s\)에서 도달 가능하므로 이를 귀납적으로 생각하면 \(S\)의 모든 정점은 결국 \(s\)에서 도달 가능하다는 것을 알 수 있습니다.
반대로 이번에는 \(s\)에서 도달 가능한 정점들이 모두 \(S\)에 들어 있는지를 알아 봅시다. 어떤 정점 \(v\)가 \(s\)에서 도달 가능하다면 분명 \(s\)에서 \(v\)로 가는 경로 \(P = \langle s = u_0, u_1, \cdots, u_{\ell-1}, u_\ell = v \rangle \)가 존재합니다. 일단 \(s = u_0\)는 \(Q\)에 처음부터 들어간 채로 시작하므로 \(S\)에 들어가 있습니다. 이제 귀납적으로 \( u_{i - 1} \)이 \(S\)에 들어갔다고 가정해 보죠. 그 말은 \(u_{i - 1}\)이 언젠가 \(Q\)에 \(\mathsf{enqueue}\)되었다는 의미이고, 따라서 이후 언젠가 \(Q\)에서 \(\mathsf{dequeue}\)될 것이라는 뜻입니다. 그때 \(u_i\)가 만약 \(Q\)에 들어 있지 않았다면 이번에 \(u_i\)가 \(\mathsf{enqueue}\)가 되겠죠. 따라서 \(u_i \in S\)가 성립합니다. ■
다음 정리는 매번 알고리즘이 유지하는 \(S\)의 정점들은 최단 경로가 결정된 상태라는 것을 말합니다. 이는 위 정리와 함께 알고리즘이 최단 경로 트리를 출력한다는 것을 보여 줍니다.
정리 3. \(S\)의 최적성
알고리즘이 수행되는 동안 계속 유지하는 \(S\)의 모든 정점은 최단 경로가 결정된 상태이다. 다시 말해, 어떤 정점 \(v\)가 \(S\)에 들어가면 그때의 \( d[v] \)는 \(s\)에서 \(v\)까지의 최단 경로의 비용이며, \(v \neq s\)면 \( \pi(v) \)는 최단 경로 상 직전의 정점이다. 이는 알고리즘이 끝날 때까지 유지된다.
[증명] 알고리즘이 수행되는 시간의 경과에 따라서 귀납적으로 보이겠습니다. 가장 먼저 \(S\)에 들어가는 정점은 \(s\)입니다. 그때의 \(d[s]\)는 0입니다. 이는 \(s\)에서 \(s\)까지 가는 경로는 \( \langle s \rangle \) 그 자체라는 사실을 통해 \(s\)에서 \(s\)까지의 최단 경로의 비용이 그때의 \(d[s]\)와 동일하다는 것을 알 수 있습니다. 이후에 \(d[s]\)가 수정이 되려면 단계 5-iii의 조건을 만족해야 하는데 입력으로 주어지는 모든 간선의 비용이 음이 아니라는 사실 때문에 \(d[s] = 0\)은 그대로 계속 고정된 채로 알고리즘이 끝날 것입니다. \(s\)에 대해서는 \(\pi(s)\)를 정의하지 않습니다. 이것으로 기저 조건이 만족한다는 것을 알 수 있습니다.
이후 언젠가 \(v\)가 \(S\)에 들어가는 때를 생각해 봅시다. 귀납 가정(induction hypothesis)으로서 들어가기 전의 \(S\)의 모든 정점들은 정리의 조건을 모두 만족한다고 가정하겠습니다. 이제 \(v\)가 \(S\)에 들어갈 때 \(d[v]\)가 실지로 \(s\)에서 \(v\)까지의 최단 경로의 비용이고, 들어갈 당시의 \( \pi(v) \)가 최단 경로 상의 직전 정점이라는 것을 보이겠습니다. 편의 상 당시의 \( \pi(v) \)를 \(u\)라고 부르겠습니다. 알고리즘이 동작하는 방식을 잘 따져 보면 \(u\)는 \(v\)가 \(S\)에 들어갈 때 이미 \(S\)에 들어 있었다는 것을 알 수 있습니다.
먼저 들어갈 당시의 \( d[v] \)가 실제 최단 경로의 비용임을 보이죠. 일단 \(d[v]\)의 값은 어떻게 결정되었을까요? 이는 \(u\)가 \(S\)에 들어갈 때 그에 인접한 정점들에 대해 단계 5-iii을 진행할 때 결정됩니다. 따라서 귀납 가정을 통해 \(d[v]\)는 \(s\)에서 \(u\)까지의 최단 경로로 온 다음 \(u\)에서 \(v\)로 향하는 경로의 비용을 의미합니다. 해당 경로를 \(P\)라고 부르겠습니다. 우리의 목표는 \(P\)가 실제 최단 경로임을 보이는 것이죠.
\(P\)가 최단 경로가 아니라고 하겠습니다. 그러면 \(P\)와 같지 않은 \(s\)에서 출발하여 \(v\)에 도달하는 최단 경로가 있을 것입니다. 이를 \(P'\)이라고 부르죠. 이에 집중해 봅시다. 이 경로도 \(s\)에서 출발하여 \(v\)로 도달하는 경로입니다. 이때 \(s\)는 원래 \(S\)에 들어간 상태이고 \(v\)는 (아직은) 들어가지 않은 상태이므로 분명히 \(P'\) 위에는 현재 \(S\)에 들어 있는 정점에서 \(S\)에 들어 있지 않은 정점으로 향하는 간선이 적어도 하나는 존재합니다. 그것들 중에서 가장 처음 나오는 간선을 \( \langle x, y \rangle \)라고 부르겠습니다.

\(P'\)은 \(s\)에서 \(v\)로 향하는 최단 경로라고 하였으므로, 정리 1을 반복해서 적용하면 \(P'\)을 따라 \(x\)까지 가는 경로도 \(s\)에서 \(x\)로 향하는 최단 경로이며 \(y\)까지 가는 경로도 \(y\)로 향하는 최단 경로입니다. 또한, \(x\)는 이미 \(S\)에 들어가 있는 상태이므로 귀납 가정에 의해 \(d[x]\)는 \(x\)까지의 최단 경로의 비용을 저장하고 있습니다. 따라서 현재 \(y\)는 우선순위 큐 \(Q\)에 들어간 상태이고 \(d[y]\)의 값은 \(y\)까지의 최단 경로의 비용이라는 사실을 이끌어 낼 수 있습니다.
여기서 \(d[y]\)의 값을 잘 생각해 보시기 바랍니다. 입력된 간선 비용은 음이 아니므로 분명 \( d[y] \)는 \(c(P')\)보다 크지 않습니다. 그런데 앞에서 \(P\)가 최단 경로가 아니라고 가정하였으므로, \[ d[y] \leq c(P') < c(P) = d[v] \]가 됩니다. 이는 이번에 \(v\)를 \(Q\)에서 \( \mathsf{dequeue} \)했다는 것에 모순이 되지요. 따라서 \(P\)는 최단 경로가 되어야 합니다.
\(P\)가 최단 경로이므로 이후에 알고리즘이 \( \pi(v) \)의 값을 바꾸는 일은 없습니다. 따라서 \(v\)가 \(S\)에 들어갈 때의 \(d[v]\)와 \(\pi(v)\)는 계속 유지됩니다. 앞에서 \(\pi(v) = u\)는 실제로 최단 경로 상 직전 정점임을 보였습니다. 이것으로 \(v\)가 \(S\)에 들어갈 떄 \( d[v] \)가 최단 경로의 비용이라는 점, \( \pi(v) \)는 최단 경로 상 직전 정점이라는 점, 그리고 이들이 알고리즘이 끝날 때까지 유지된다는 것이 증명됩니다. ■
이것으로 알고리즘이 최단 경로 트리를 반환한다는 것을 증명하였습니다. 이제는 알고리즘의 수행 시간을 분석해 보도록 하겠습니다. 이를 위해서는 다음 정리를 확인해야 합니다.
정리 4. 알고리즘 1에서 우선순위 큐의 동작 횟수
알고리즘 1에서 \(Q\)는 \(\mathsf{dequeue}\)를 최대 \(|V|\)번, \( \mathsf{enqueue} \)와 \( \mathsf{decreasekey} \)는 합해서 최대 \(|E|\)번 수행한다.
[증명] 각 정점이 한 번 \(Q\)에 들어갔다가 나오면 다시는 들어가지 않음을 보이겠습니다. 그러면 \(\mathsf{dequeue}\)가 최대 \(|V|\)번이 된다는 것은 바로 증명됩니다. 알고리즘에서 어떤 정점 \(v\)가 \(Q\)에 들어가기 위해서는 단계 5-iii의 조건을 만족해야 합니다. 그러나 \(v\)가 \(Q\)에서 나오는 순간 \(S\)에 들어가며, 정리 3에 의해 \(d[v]\)는 최단 경로의 비용이므로 단계 5-iii의 조건을 만족할 수 없습니다.
이제 \(\mathsf{enqueue}\)와 \(\mathsf{decreasekey}\)가 합해서 최대 \(|E|\)번 수행된다는 것을 보이겠습니다. 이 동작들은 언젠가 \(u\)가 \(Q\)에서 \(\mathsf{dequeue}\)되었을 때, 거기서 나가는 방향으로 인접한 정점들 중 단계 5-iii의 조건을 만족하는 정점들에 대해서 수행이 됩니다. 앞에서 \(u\)가 한 번 \(Q\)에서 나오면 다시 들어가지 않는다고 했으므로, 해당 정점을 고려할 때 두 동작의 횟수는 아무리 많아도 나가는 방향으로의 차수(out-degree)를 넘지 못합니다. 각 정점에 대해 차수를 모두 더한 것은 \(|E|\)이므로 명제의 증명이 완성됩니다. ■
정리 4를 통해 \(Q\)의 실제 구현에 따른 알고리즘 1의 수행 시간을 다음과 같이 구할 수 있습니다.
| 본문의 쉬운 구현 | 이진 힙 | 피보나치 힙 | |
| 수행 시간 | \(O(|E| + |V|^2)\) | \( O((|E| + |V|) \log |V| ) \) | \( O(|E| + |V| \log |V|) \) |
위 표에서 흥미로운 사실은 만약 입력된 그래프가 매우 밀집(dense)되어 있다면 (예를 들어, \( |E| = \Omega(|V|^2) \)) 본문의 쉬운 구현을 사용한 알고리즘 1이 이진 힙을 사용한 알고리즘 1보다 시간 복잡도 상으로 더 좋다는 점입니다. 반대로 그래프가 희소(sparse)한 경우에는 (예를 들어, \(|E| = O(|V|)\)) 이진 힙이 본문의 쉬운 구현보다 더 좋은 수행 시간을 보입니다. 피보나치 힙은 어떤 경우에서든 가장 좋은 성능을 보이고요.
실제로는 어떻게 될지 궁금하네요. 아마도 피보나치 힙은 구현 자체가 복잡해서 현실적으로는 가장 느릴 것 같고요, 밀집 그래프에서도 어쩌면 이진 힙이 본문의 쉬운 구현보다 더 좋지 않을까 생각도 듭니다.
마치며
이것으로 음이 아닌 비용만 있는 그래프에서의 최단 경로 문제를 벨만-포드 알고리즘의 세제곱 시간보다 빠른 제곱 시간에 해결하는 다익스트라의 알고리즘에 대해서 알아 보았습니다. 이 알고리즘은 여러 분야에서 자주 사용되니 잘 알아 두시면 좋겠습니다.
읽어 주셔서 고맙습니다. :)
'조합론적 최적화 > Shortest path' 카테고리의 다른 글
| A* 알고리즘 (A* Search Algorithm) (3) | 2023.11.25 |
|---|---|
| 최단 경로 문제 & 벨만-포드 알고리즘 (Shortest Path Problem & Bellman-Ford Algorithm) (1) | 2021.08.22 |

