
최대 흐름 문제(maximum flow problem)는 어떤 방향 그래프(directed graph)와 간선 위의 용량(capacity)으로 정의되는 흐름 네트워크(flow network)에서 시점(source)부터 종점(sink)까지 최대한 많은 양의 물을 흘리는 방법을 찾는 문제입니다. 이 문제는 이론적으로는 물론 산업적으로도 깊이 연구된 매우 중요한 조합론적 최적화 문제입니다. 제 블로그에서도 현재까지 다섯 개의 글을 적었을 만큼 매우 비중 있게 다룬 주제입니다.
이번 포스트에서는 이 문제를 보다 확장을 시켜 보고자 합니다. 원래 문제에서는 각 간선에 이 이상은 흘릴 수 없다는 제약을 주는 용량만 있었습니다. 하지만 경우에 따라서는 각 간선마다 적어도 이 정도는 흐르고 있어야 한다는 일종의 필요량을 정의해 볼 수 있겠습니다. 또한, 원래는 시점과 종점에서만 각각 물을 무한히 생산하고 소비할 수 있고, 나머지 정점에서는 흐름이 보존되어야 하였습니다. 하지만 이번에는 모든 정점에서 일정한 양을 생산 혹은 소비해야 한다는 제약을 두어 보겠습니다.
이 상황에서 우리의 목표는 각 간선의 용량과 필요량을 모두 만족하면서 모든 정점의 생산량과 소비량을 충족시켜 주는 흐름을 찾는 것입니다. 원래 문제의 목표는 흐름의 양이 최대가 되는 흐름을 찾는 것이 목표였지만, 이번에는 다양한 제약 조건 때문에 가능한 흐름을 찾는 것임을 확인하세요. 이 문제는 서큘레이션 문제(circulation problem)라고 불립니다. 서큘레이션, 즉, 순환이라고 불리는 이유는 다음과 같습니다. 모든 정점에서 생산되는 물이나 소비되는 물이 없다고 해 보죠. 하지만 각 간선마다는 반드시 흘러야 하는 양이 정해집니다. 따라서 이 제약을 만족시키기 위해서는 폐쇄된 네트워크에서 물이 순환을 하는 구조여야 합니다. 다만 제 블로그 전반에 걸쳐서 순환은 그래프의 사이클(cycle)을 지칭할 때 사용하고 있습니다. 따라서 본문에서는 구분을 위해 서큘레이션이라고 부릅니다.
이 문제를 어떻게 해결할 수 있을까요?
문제 정의
먼저 문제를 엄밀히 정의해 보겠습니다. 입력은 다음과 같이 주어집니다.
- 방향 그래프 \(G = (V, E)\)
- 용량 \(c : E \to \mathbb{R}_+\)
- 하한(lower bound) \(\ell : E \to \mathbb{R}_+\)
- 공급량(supply) \(q : V \to \mathbb{R}\)
방향 그래프와 용량은 기존의 최대 흐름 문제에서 본 것과 동일한 의미입니다. 하한은 해당 간선에 반드시 흘러야 하는 흐름의 양을 정의합니다. 공급량은 말 그대로 각 정점에서 생산되는 물의 양을 뜻합니다. 다만, 공급량은 음수일 수 있고, 이때는 해당 정점이 물을 소비하는 수요량(demand)을 나타냅니다.
우리의 목표는 아래의 두 조건을 만족하는 서큘레이션 \(f : E \to \mathbb{R}_+\)를 찾는 것입니다.
- 용량·하한 제약: 임의의 간선에 흐르는 양은 항상 각 간선의 하한과 용량을 준수한다. 다시 말해, 간선 \(e \in E\)에 대해, \(\ell(e) \leq f(e) \leq c(e)\)이다.
- 흐름 보존 제약: 모든 정점에 대해 그 정점에서 흘러 나가는 양은 그 정점에서 생산된 양과 그 정점으로 흘러 들어오는 양과 동일하다. 즉, 임의의 \(v \in V\)에 대해, \[ \sum_{e \text{ out of } v} f(e) - \sum_{e \text{ into } v} f(e) = q(v)\]를 만족한다.
용량·하한 제약은 직관적으로 받아들일 수 있겠습니다. 흐름 보존 제약은 정점에서 물이 소비되는 경우에도 성립함을 확인하시기 바랍니다. 최대 흐름 문제에서는 양이 최대인 흐름을 찾는 것이었지만, 이 문제에서는 간선의 하한이 비슷한 효과를 제공하므로 위 조건을 만족하는 아무 서큘레이션을 찾기만 하면 됩니다.
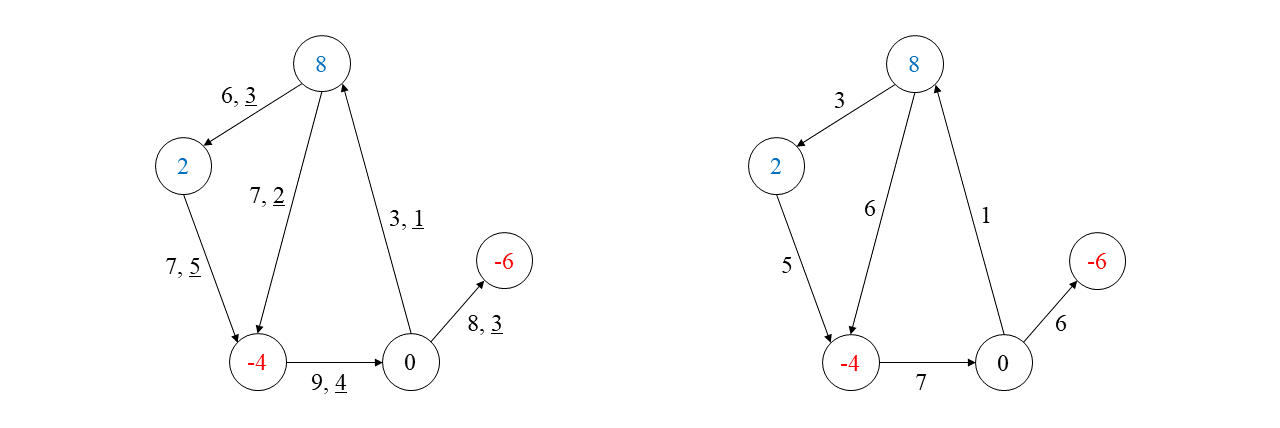
어떤 간선의 하한이 용량보다 크다면 해당 간선의 용량·하한 제약을 만족시킬 수 없습니다. 따라서, 임의의 간선 \(e \in E\)에 대해, \(\ell(e) \leq c(e)\)를 만족해야 합니다. 또한 입력으로 주어지는 네트워크는 폐쇄된 시스템이어서 정점들에서 생성된 모든 물은 다른 정점들에서 모두 소비되어야 합니다. 그러므로 \( \sum_{v \in V} q(v) = 0 \)을 만족해야 합니다. 이제부터는 입력이 위 항목들을 모두 만족한다고 가정하겠습니다.
아래 증명에서 사용할 기호를 몇 가지 정의하겠습니다. 어떤 정점의 부분집합 \(S \subseteq V\)에 대해, \(S\)에서 \(V \setminus S\)로 나가는 간선의 집합을 \( \delta^+(S) := \{ \langle u, v \rangle \in E \mid u \in S, v \in V \setminus S \} \), 반대로 \(V \setminus S\)에서 \(S\)로 들어오는 간선의 집합을 \( \delta^-(S) := \{ \langle u, v \rangle \in E \mid u \in V \setminus S, v \in S \} \)라고 부르겠습니다. 편의 상 \(\delta^+(v) := \delta^+(\{v\})\), \( \delta^-(v) := \delta^-(\{v\}) \)를 의미합니다. 다음으로 \(c(S)\)와 \(\ell(S)\)는 각각 \(S\)에서 \(V \setminus S\)로 나가는 간선들의 용량·하한의 합 \( c(S) := \sum_{e \in \delta^+(S)} c(e)\), \(\ell(S) := \sum_{e \in \delta^+(S)} \ell(e) \)로 정의하겠습니다. 마지막으로 \(q(S)\)는 \(S\)에 속한 정점들의 공급량의 합 \( q(S) := \sum_{v \in S} q(v) \)로 정의하겠습니다.
하한이 없는 문제로 환산하기
일견 이 문제는 여러 제약이 얽혀 있어서 바로 해결하기가 쉽지 않아 보입니다. 이런 경우에 우리는 이 문제를 보다 쉬운 문제로 환산(reduce)하여 해결하고는 합니다. 이번 절에서는 일반적인 입력을 하한이 없는 입력으로 환산하는 방법을 소개하겠습니다. 다시 말해, 하한이 없는 서큘레이션 문제를 풀 수 있다면, 하한이 있는 서큘레이션 문제도 쉽게 풀 수 있다는 뜻입니다.
환산 방법은 간단합니다. 입력으로 \(G, c, \ell, q\)가 주어졌을 때, 다음을 만족하는 하한이 없는 입력 \(G, c', q'\)을 고려하면 됩니다.
- 각 간선 \(e \in E\)에 대해, \( c'(e) := c(e) - \ell(e) \)
- 각 정점 \(v \in V\)에 대해, \( q'(v) := q(v) - \sum_{e \in \delta^+(v)} \ell(e) + \sum_{e \in \delta^-(v)} \ell(e) \)
참고로 환산된 입력 역시 \(c'(e) \geq 0\), \( \sum_{v \in V} q'(v) = 0 \)을 만족합니다. 전자는 쉽게 보일 수 있습니다. 후자는 \[ \sum_{v \in V} q'(v) = \sum_{v \in V} \left[ q(v) - \sum_{e \in \delta^+(v)} \ell(e) + \sum_{e \in \delta^-(v)} \ell(e) \right] = \sum_{v \in V} q(v) - \sum_{e \in E} \ell(e) + \sum_{e \in E} \ell(e) = 0\]이어서 성립합니다.
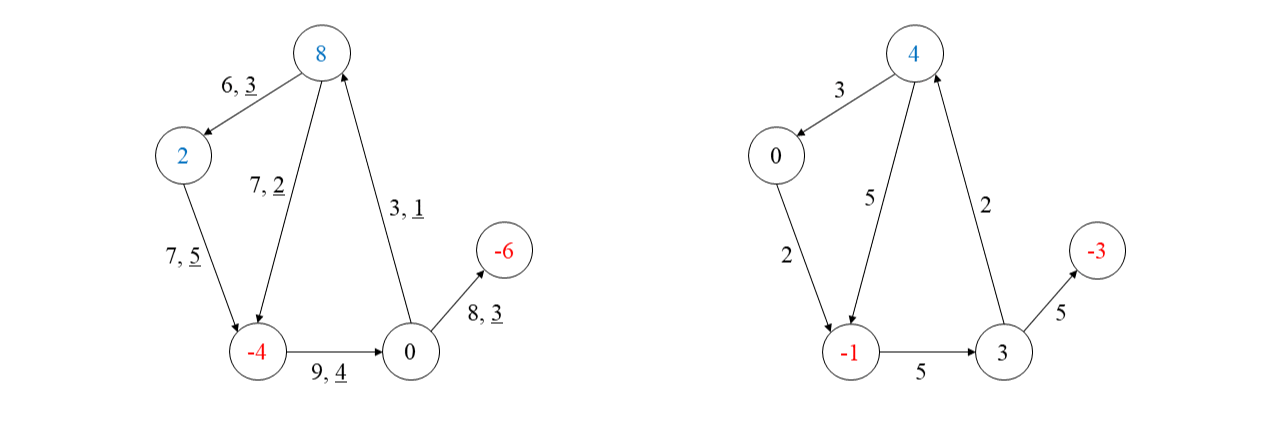
이렇게 만든 직관적인 이유를 설명해 보겠습니다. 하한은 반드시 흘러야 하는 양이므로 각 간선 \(e \in E\)마다 일단 \(\ell(e)\)를 흘려주었다고 해 보겠습니다. 그러면 각 간선마다 \(c(e) - \ell(e)\)만큼만 더 흘려줄 수 있습니다. 이 값이 곧 \(c'(e)\)에 해당합니다. 이제 각 정점 \(v \in V\)의 입장에서 생각을 해 보겠습니다. 원래 \(v\)는 \(q(v)\)만큼을 생산 또는 소비하고 있었습니다. 그런데 이제는 \(v\)에서 나가는 간선들 \(e \in \delta^+(v)\)에 대해 각각 \(\ell(e)\)씩 내보내 주어야 하므로 \(\sum_{e \in \delta^+(v)} \ell(e)\)만큼 더 소비한다고 말할 수 있습니다. 반대로 \(v\)로 들어오는 간선들 \(e \in \delta^-(v)\)에 대해서는 각각 \(\ell(e)\)씩 받게 되므로 \( \sum_{e \in \delta^-(v)} \ell(e) \)만큼 공급을 더 받는다고 볼 수 있습니다. 이를 모두 고려하면 \(q'(v)\)와 같습니다.
직관적인 이유를 살펴보았으니 이제는 엄밀히 증명해 보겠습니다. 먼저 원래 입력에 서큘레이션이 존재하면 환산된 입력에도 서큘레이션이 존재함을 보이겠습니다.
정리 1. 원래 입력 \(\implies\) 환산된 입력
원래 입력 \(G, c, \ell, q\)에 서큘레이션 \(f : E \to \mathbb{R}_+\)가 존재한다고 하자. 다음과 같이 정의된 \(f' : E \to \mathbb{R}_+\)는 환산된 입력 \(G, c', q'\)의 서큘레이션이다.
- 각 간선 \(e \in E\)에 대해, \(f'(e) := f(e) - \ell(e)\)
[증명] 각 간선 \(e \in E\)에 대해, \(f\)는 원래 입력의 서큘레이션이므로, \( \ell(e) \leq f(e) \leq c(e) \)를 만족합니다. 따라서 \( 0 \leq f'(e) \leq c(e) - \ell(e) = c'(e) \)가 성립합니다. 이것으로 \(f'\)이 용량 제약을 만족함을 알 수 있습니다.
이번에는 각 정점 \(v \in V\)에 대해, \[ \sum_{e \in \delta^+(v)} f(e) - \sum_{e \in \delta^-(v)} f(e) = q(v) \]를 만족합니다. \( f(e) = f'(e) + \ell(e) \)이므로, 위 식에 대입한 후 정리하면 \[ \sum_{e \in \delta^+(v)} f'(e) - \sum_{e \in \delta^-(v)} = q(v) - \sum_{e \in \delta^+(v)} \ell(e) + \sum_{e \in \delta^-(v)} \ell(e) = q'(v) \]가 성립합니다. 이것으로 \(f'\)이 흐름 보존 제약도 만족한다는 것을 알 수 있습니다. ■
환산이 올바르기 위해서는 환산된 입력에 서큘레이션이 존재하면 원래 입력에도 서큘레이션이 존재한다는 것을 보여야 합니다. 위 정리의 증명을 대칭적으로 적용하면 쉽게 아래 정리를 이끌어 낼 수 있습니다.
정리 2. 환산된 입력 \(\implies \) 원래 입력
환산된 입력 \(G, c', q'\)에 서큘레이션 \(f' : E \to \mathbb{R}_+\)가 존재한다고 하자. 다음과 같이 정의된 \(f : E \to \mathbb{R}_+\)는 원래 입력 \(G, c, \ell, q\)의 서큘레이션이다.
- 각 간선 \(e \in E\)에 대해, \(f(e) := f'(e) + \ell(e)\)
최대 흐름 문제로 환산하기
이전 절에서 우리는 하한이 존재하는 서큘레이션 문제를 하한이 존재하지 않는 서큘레이션 문제로 환산할 수 있음을 보였습니다. 그러므로 이제부터 입력은 \(G, c, q\)로만 이루어져 있다고 해 보겠습니다. 이제는 입력에 용량밖에 없으므로 우리가 원래 잘 알고 있는 최대 흐름 문제와 흡사해 보입니다. 이번 절에서는 실지로 하한이 없는 서큘레이션 문제를 최대 흐름 문제로 환산할 수 있음을 보이겠습니다.
원래 입력의 각 간선의 용량은 최대 흐름 문제에서의 용량과 비슷하게 작동할 것으로 보입니다. 최대 흐름 문제와 다른 점을 꼽자면 바로 각 정점마다 존재하는 공급량·수요량입니다. 최대 흐름 문제에는 대신 시점과 종점이 있습니다. 따라서 시점에서 물을 생산하는 정점으로 그것의 공급량만큼 흘려주고, 반대로 물을 소비하는 정점에서 종점으로 그것의 수요량만큼 흘려준다면 최대 흐름 문제에서처럼 시점과 종점에서만 각각 생산·소비하고 나머지 정점에서는 흐름을 보존하게 된다는 것을 기대할 수 있습니다.
이 아이디어를 구현해 봅시다. 원래 입력 \(G = (V, E), c, q\)에 대해, 이번에는 다음과 같이 정의된 최대 흐름 문제의 입력 \(G'=(V', E'), c', s, t\)를 고려해 보겠습니다.
- \(V' := V \cup \{s, t\}\)
- \(E' := E' \cup \{\langle s, v \rangle \mid q(v) > 0 \} \cup \{ \langle v, t \rangle \mid q(v) < 0 \} \)
- 각 간선 \(e \in E\)에 대해서는 \(c'(e) := c(e)\)
- \(s\)에 딸린 간선 \(\langle s, v \rangle \in E'\)에 대해서는 \( c'(s, v) := q(v) \)
- \(t\)에 딸린 간선 \( \langle v, t \rangle \in E' \)에 대해서는 \(c'(v, t) := -q(v)\)
이때, \(t\)는 공급량이 음수인 \(v\)로부터만 인접하므로 \( c'(v, t) > 0 \)입니다.
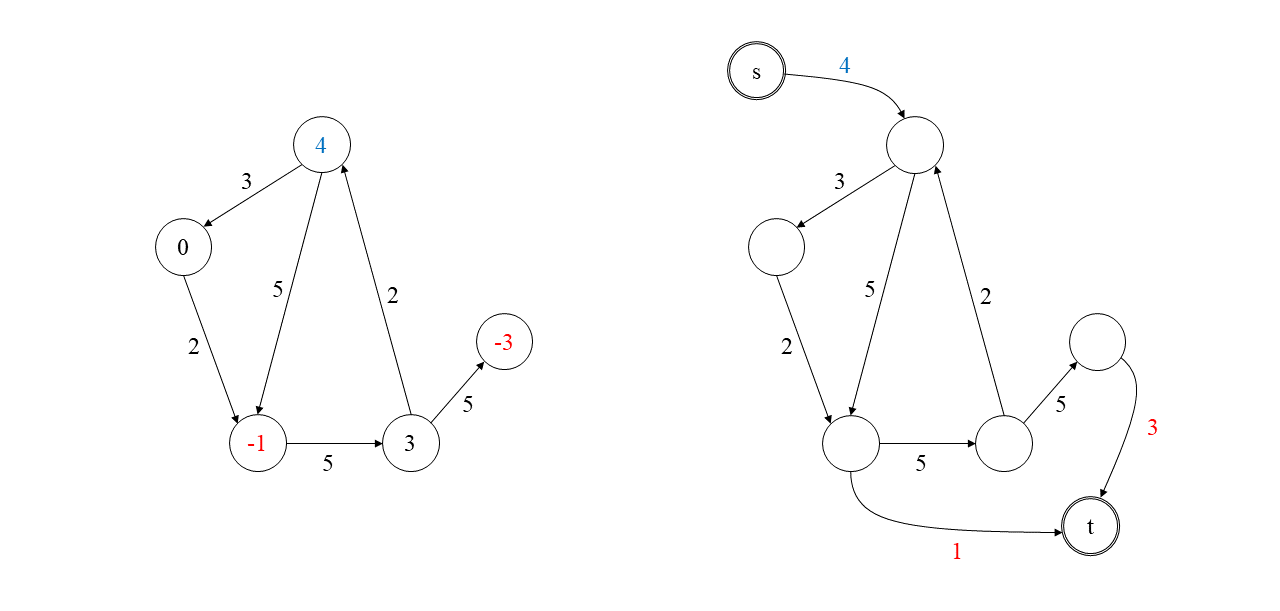
원래 입력에서 정점들의 총공급량을 \(Q := \sum_{v \in V : q(v) > 0} q(v)\)라고 하겠습니다. 이는 가정에 의해 총수요량과 동일합니다. 서큘레이션 문제에서는 모든 정점이 정확히 \(q(v)\)를 생산(혹은 \(-q(v)\)를 소비)해야 하므로 최대 흐름 문제에서 \(s\)에 딸린 모든 간선과 \(t\)에 딸린 모든 간선이 포화되어야(saturated) 할 것입니다. 따라서 원래 입력에 서큘레이션이 존재하기 위해서는 환산된 입력에 흐름양이 \(Q\)인 흐름이 존재해야 할 것입니다. 이것이 곧 원래 입력에서 서큘레이션이 존재할 필요충분조건이 됩니다.
정리 3. 원래 입력 \(\iff\) 환산된 입력
원래 입력 \(G, c, q\)에 서큘레이션 \(f:E \to \mathbb{R}_+\)가 존재한다고 하자. 그러면 다음과 같이 정의된 \(f' : E' \to \mathbb{R}_+\)는 환산된 입력 \(G', c', s, t\)에서 흐름양이 \(Q\)인 \(s \text{-} t\) 흐름이다.
- 각 간선 \(e \in E\)에 대해, \(f'(e) := f(e)\)
- \(s\)에 딸린 간선 \(\langle s, v \rangle \in E'\)에 대해, \(f'(s, v) := q(v)\)
- \(t\)에 딸린 간선 \(\langle v, t \rangle \in E'\)에 대해, \(f'(v, t) := -q(v)\)
반대로 환산된 입력 \(G', c', s, t\)에서 흐름양이 \(Q\)인 \(s \text{-} t\) 흐름 \(f'\)이 존재하면, \(f'\)에서 \(E\)에 해당하는 간선만 고려한 \(f\)는 원래 입력 \(G, c, q\)의 서큘레이션이다.
증명은 앞에서 논의한 내용을 엄밀한 용어로 풀어 적는 것에 불과하므로 생략합니다.
알고리즘
이전 절에서 살펴본 내용을 토대로 우리는 일반적인 서큘레이션 문제를 해결하는 알고리즘을 다음과 같이 얻을 수 있습니다.
알고리즘 1. 서큘레이션 알고리즘
입력: 방향 그래프 \(G=(V, E)\), 간선 용량 \(c\), 간선 하한 \(\ell\), 정점 공급량 \(q\)
출력: 서큘레이션
- 입력 \(G, c, \ell, q\)를 하한이 없는 서큘레이션 입력 \(G, c', q'\)으로 변환한다.
- 입력 \(G, c', q'\)을 최대 흐름 문제 입력 \(G', c'', s, t\)로 변환한다.
- \(G', c'', s, t\)의 최대 흐름 \(f''\)을 구한다.
- 만약 \(f''\)의 흐름양이 \(\sum_{v \in V : q'(v) > 0} q'(v)\)보다 작으면 서큘레이션이 없다고 반환한다.
- 그렇지 않다면 \(f''\)을 원래 입력 \(G, c, \ell, q\)의 서큘레이션으로 변환하여 반환한다.
이 알고리즘의 수행 시간을 분석해 보겠습니다. 단계 1은 \(O(|E|)\) 시간이면 충분합니다. 반면 단계 2의 경우, \(G'\)의 정점 개수는 \(|V| + 2\)이며, 간선의 개수는 원래 있던 \(E\)에 \(s\)와 \(t\)에 딸린 간선들이 추가되어야 하므로 최대 \(|E| + |V|\)가 됩니다. 단계 5는 모두 \(O(|E|)\) 시간에 할 수 있습니다. 따라서 다음의 정리를 이끌어 낼 수 있습니다.
정리 4. 알고리즘 1의 수행 시간
정점의 개수가 \(n\), 간선의 개수가 \(m\)인 흐름 네트워크에서 최대 \(s \text{-} t\) 흐름을 구하는 데 필요한 시간을 \(r(n, m)\)이라고 하자. 알고리즘 1은 \(O(r(|V|, |V| + |E|))\) 시간에 동작한다.
최대 흐름 최소 절단 정리와의 관계
최대 흐름 최소 절단 정리(max-flow min-cut theorem)는 최대 흐름의 양과 최소 절단의 용량은 동일하다는 것으로 최대 흐름의 최적성(optimality)을 판단하는 증거가 됩니다. 우리는 지금껏 서큘레이션 문제를 최대 흐름 문제로 환산하여 해결하는 방법을 공부하였습니다. 따라서 서큘레이션에도 최대 흐름 최소 절단 정리를 도입하면 흥미로운 성질을 얻을 수 있을 것입니다.
먼저 하한이 존재하지 않는 서큘레이션 문제를 고려해 보겠습니다. 앞에서 우리는 원래 입력 \(G, c, q\)에 대해, 흐름 네트워크 \(G', c', s, t\)를 만들었습니다. 또한, \(G, c, q\)에 서큘레이션이 존재하기 위한 필요충분조건이 환산된 흐름 네트워크 \(G', c', s, t\)에 흐름양이 \(Q = \sum_{v \in V : q(v) > 0} q(v)\)인 \(s \text{-} t\) 흐름이 존재하는 것이라 점을 보였습니다. 최대 흐름 최소 절단 정리에 의해, 환산된 입력에 \(Q\) 이상의 \(s \text{-} t\) 흐름이 존재하기 위한 필요충분조건은 환산된 입력에서 임의의 \(s \text{-} t\) 절단 \((S, V' \setminus S)\)에 대해, 그것의 절단 용량이 항상 \(Q\) 이상이라는 것임을 유도할 수 있습니다.
그렇다면 환산된 입력에서 \((S, V' \setminus S)\)의 절단 용량은 얼마일까요? 절단 용량은 \(S\)에서 \(V' \setminus S\)로 나가는 간선의 용량만을 더한 것입니다. 그러한 간선은 다음의 총 세 가지 경우로 나눌 수 있습니다.
- \(u \in V \cap S\), \(v \in V \setminus S\)인 \( \langle u, v \rangle \in E \)
- \(v \in V \setminus S\), \(q(v) > 0\)인 \( \langle s, v \rangle \)
- \(v \in S\), \(q(v) <0\)인 \( \langle v, t \rangle \)
따라서 \((S, V' \setminus S)\)의 절단 용량이 \(Q\) 이상이라는 뜻은 원래 입력에서 \[ \sum_{e \in \delta^+(S)} c(e) + \sum_{\substack{v \in V \setminus S :\\ q(v) > 0}} q(v) - \sum_{\substack{v \in S :\\ q(v) < 0}} q(v) \geq Q = \sum_{\substack{v \in V :\\ q(v) > 0}} q(v) \]를 의미하게 됩니다. 좌변의 \(q(v)\)들을 우변으로 넘겨 주면, \[ c(S) = \sum_{e \in \delta^+(S)} c(e) \geq \sum_{\substack{v \in V: \\ q(v) > 0}} q(v) - \sum_{\substack{v \in V \setminus S: \\ q(v) > 0}} q(v) + \sum_{\substack{v \in S: \\ q(v) < 0}} q(v) = \sum_{v \in S} q(v) = q(S) \]를 얻게 됩니다.
정리 5. 하한이 없을 때 서큘레이션이 존재할 필요충분조건
하한이 없는 서큘레이션 문제에 대해, 입력 \(G, c, q\)에 서큘레이션이 존재할 필요충분조건은 임의의 \(S \subseteq V\)에 대해 \(c(S) \geq q(S)\)를 만족하는 것이다.
이 정리를 직관적으로 해석해 보겠습니다. 어떤 정점의 부분집합 \(S\)에 대해, \(q(S)\)는 \(S\) 내에서 모두 소비되지 못한 잉여 공급량으로 볼 수 있습니다. 서큘레이션이 존재하기 위해서는 이 잉여 공급량을 \(S\)의 바깥으로 내보내야 합니다. \(S\)에서 바깥으로 나가는 간선들의 총용량은 \(c(S)\)와 같습니다. 그러므로 서큘레이션이 존재하기 위해서는 당연히 \(c(S) \geq q(S)\)를 만족해 주어야 하겠습니다.
하한이 존재하는 일반적인 서큘레이션 문제에 대해서도 생각해 봅시다. 앞에서 우리는 \(G, c, \ell, q\)를 하한이 없는 입력 \(G, c', q'\)으로 환산시켰습니다. 정리 5에 의해 환산된 입력에 서큘레이션이 존재할 필요충분조건은 임의의 \(S \subseteq V\)에 대해, \(c'(S) \geq q'(S)\)라는 것을 알고 있습니다. 먼저, \(c'(S) = c(S) - \ell(S)\)입니다. \(q'(S)\)는 \[ \sum_{v \in S} q'(v) = \sum_{v \in S} \left[ q(v) - \sum_{e \in \delta^+(v)} \ell(e) + \sum_{e \in \delta^-(v)} \ell(e) \right] = q(S) - \ell(S) + \ell(V \setminus S) \]와 같습니다. 그러므로 하한이 있는 문제에 대해서도 다음과 같은 필요충분조건을 얻을 수 있습니다.
정리 6. 서큘레이션이 존재할 필요충분조건
일반적인 서큘레이션 문제에 대해, 입력 \(G, c, \ell, q\)에 서큘레이션이 존재할 필요충분조건은 임의의 \(S \subseteq V\)에 대해 \(c(S) \geq q(S) + \ell(V \setminus S)\)를 만족하는 것이다.
이 정리 또한 직관적으로 해석할 수 있습니다. 앞에서 \(q(S)\)는 \(S\) 내에서 소비되지 못한 잉여 공급량이라고 하였습니다. \(\ell(V \setminus S)\)는 \(V \setminus S\)에서 \(S\)로 반드시 들어오는 양입니다. 따라서 \(S\) 내에는 \(q(S) + \ell(V \setminus S)\)만큼의 잉여 공급량이 존재합니다. 서큘레이션이 존재하기 위해서는 \(c(S)\)가 잉여 공급량을 충분히 감당할 수 있어야 합니다.
마치며
이것으로 서큘레이션 문제에 대한 포스팅을 모두 마칩니다. 이번 포스팅을 적게 된 계기는 부끄럽게도 서큘레이션 문제를 잘 알고 있다고 생각하고 있었는데, 학부 알고리즘 수업 과제를 채점하는 중에 부족함을 깨달았기 때문입니다. 꼼꼼히 살피지 않고 넘어갔더라면 채점이 잘못되는 큰 불상사가 발생할 뻔하였습니다. 다시 공부한 김에 이렇게 글을 남깁니다.
고맙습니다.
참고 자료
[1] Jon Kleinberg and Eva Tardos. Algorithm design. Pearson Education, 2013.
'조합론적 최적화 > Flow & Circulation' 카테고리의 다른 글
| 디니츠의 알고리즘 (Dinitz' Algorithm) (7) | 2021.02.27 |
|---|---|
| 에드몬즈-카프 알고리즘 (Edmonds-Karp Algorithm) (6) | 2021.02.21 |
| 포드-풀커슨 방법 (Ford-Fulkerson Method) (3) | 2020.08.30 |
| 최대 흐름 최소 절단 정리 (Max-Flow Min-Cut Theorem) (13) | 2020.08.29 |
| 최대 흐름 문제 이해하기 (Maximum Flow Problem) (20) | 2020.08.29 |



