얼마 전 친한 형님이 또 재미있는 문제를 하나 소개해주었습니다. 처음에 전 그 문제가 NP-난해일 것이라고 생각했지만, 토의를 거친 끝에 그 문제가 순환이 없는 방향 그래프(directed acyclic graph, DAG)에서 최소 경로 덮개(minimum path cover)를 찾는 문제로 환원될 수 있다는 것을 찾아냈습니다. 또한 놀랍게도, 일반적인 그래프에서 최소 경로 덮개를 찾는 문제는 NP-난해하지만, DAG에서는 다항 시간에 찾을 수 있다는 것도 알게 되었습니다. Bipartite matching을 활용하면 된다는데, 곰곰이 생각해 보니 쉽게 보일 수 있더군요. 이번 포스트에서는 이에 대해서 간단히 알아보도록 하겠습니다.
문제를 엄밀히 정의하도록 하겠습니다. 입력으로는 방향이 있는 그래프(directed graph) \(G = (V, A)\)가 주어집니다. 우리의 목표는 이 그래프의 모든 정점을 서로 겹치지 않는 경로(path)들로 뒤덮는 것입니다. 좀더 엄밀히 말하면, 다음을 만족하는 단순 경로들의 집합 \(\mathcal{C}\)를 찾는 것입니다.
- 임의의 두 단순 경로 \(P, P^\prime \in \mathcal{C}\)에 대해, \(V(P) \cap V(P^\prime) = \emptyset\)
- \( \bigcup_{P \in \mathcal{C}} V(P) = V \)
이때, \( \mathcal{C} \)에는 길이가 \(0\)인 경로(즉, 정점 하나로 이루어진 경로)가 포함될 수 있습니다. 다시 말해, 모두 길이가 0인 경로를 고르는 것도 가능한 방법 중 하나입니다. 하지만 이는 너무 자명하죠? 따라서, 위 조건을 만족하는 \(\mathcal{C}\) 중에서 그 크기(즉, \(|\mathcal{C}|\))가 가장 작은 것이 우리의 최종 목표가 되겠습니다.
만약 아무런 조건도 없는 임의의 그래프가 입력으로 주어진다면, 이 그래프에서 최소 경로 덮개를 찾는 문제는 NP-난해(NP-hard)합니다. 왜냐하면, 어떤 그래프 위에 모든 정점을 정확히 한 번씩 지나는 경로가 존재하는지를 판단하는 문제가 NP-완전(NP-complete)하기 때문입니다. 만약 임의의 그래프에 대해 최소 경로 덮개를 다항 시간에 구하는 알고리즘이 존재하면, 저 문제의 입력에 대해 이 알고리즘을 수행한 후, 출력된 \( \mathcal{C} \)의 크기가 \(1\)이면 그러한 경로가 존재한다고, 그렇지 않으면 존재하지 않는다고 반환하는 것으로 저 문제를 다항 시간에 해결할 수 있습니다. 따라서 P = NP가 아닌 한, 임의의 그래프에서 최소 경로 덮개를 다항 시간에 구하는 것은 불가능합니다.
흥미롭게도 그래프에 순환이 없으면 이 문제는 다항 시간에 해결할 수 있게 됩니다. 바로 bipartite matching을 이용해서 말이죠. 이에 바로 들어가기 전에, 아래의 증명에서 요긴하게 쓰일 정리를 하나 증명하고 넘어가겠습니다. 여기서 \(n := |V|\)를 의미합니다.
정리 1. 경로 길이의 합에 관한 등식
\(G\)의 어떤 path cover \( \mathcal{C} \)에 대해, 항상 \[ n = |\mathcal{C}| + \sum_{ P \in \mathcal{C} } |P| \]가 만족한다.
[증명] \(V\)를 어떤 경로의 시작 정점의 부분집합 \(V_s\)와 그렇지 않은 정점들의 부분집합 \(V_t\)로 나누겠습니다. 다시 말해, \[ \begin{array}{rl} V_s & := \{ v \in V : \exists P = \langle v, \cdots \rangle \in \mathcal{C} \} \\ V_t & := \{ v \in V : \exists \langle u, v \rangle \in P \text{ for some } P \in \mathcal{C} \} \end{array} \]로 표현할 수 있겠습니다. 그러면 둘은 \( V_s \cap V_t = \emptyset, V_s \cup V_t = V \)를 만족하는 partition이 됩니다. 즉, \[ |V| = |V_s| + |V_t| \]를 만족하게 되죠. 이때, \(V_s\)는 경로의 시작점들의 집합이므로 \( |V_s| = |\mathcal{C}| \)임을 알 수 있고, 어떤 경로의 한 간선의 끝점이 \(V_t\)에 들어오는 것이므로 \( |V_t| = \sum_{P \in \mathcal{C}} |P| \)임을 알 수 있습니다. 이를 조합하면 정리의 등식을 이끌어낼 수 있습니다. □
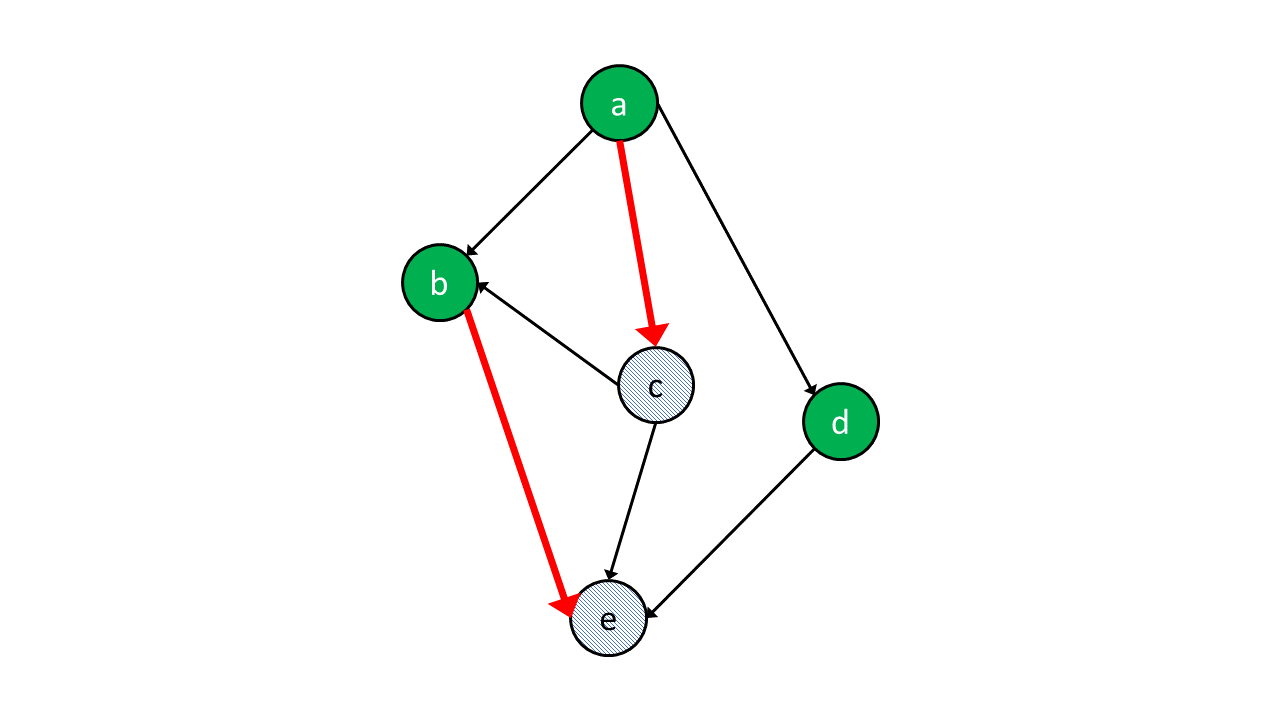
이제 입력된 순환이 없는 \(G = (V, A)\)에 대해서, 다음을 만족하는 보조 그래프 \(H = (L \cup R, E)\)를 만들어 봅시다.
- \( L := \{ v^\ell : v \in V \} \)
- \( R := \{ v^r : v \in V\} \)
- \( E := \{ (u^\ell, v^r) : \langle u, v \rangle \in A \} \)
참고로 \(H\)는 bipartite graph입니다.
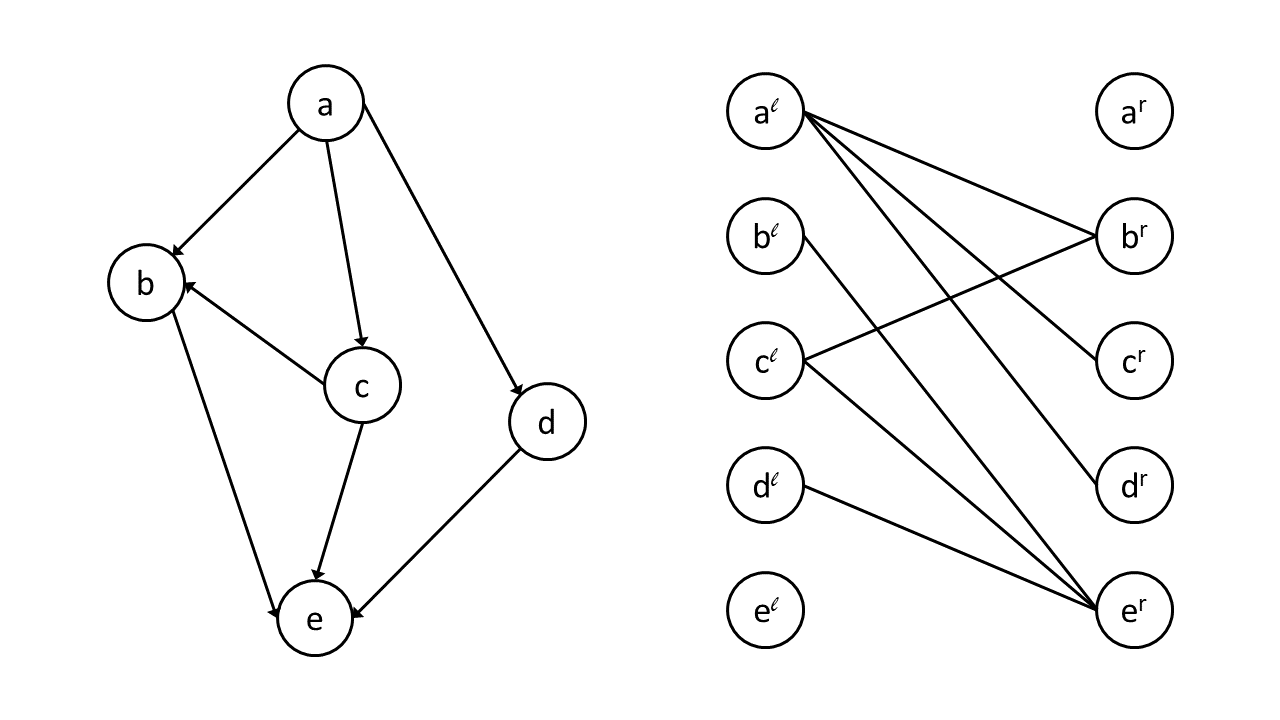
그러면 \(G\) 위의 임의의 path cover가 \(H\)의 matching과 매우 밀접한 연관이 있다는 사실을 알 수 있습니다.
정리 2. Path cover to matching
\(G\)의 어떤 minimum path cover를 \(\mathcal{C}\)라고 하면 \(H\)에는 최소한 크기가 \(n - |\mathcal{C}|\)인 matching이 존재한다.
[증명] 다음과 같이 \(M\)을 정의해 보도록 하죠. \[ M := \{ (u^\ell, v^r) : \langle u, v \rangle \in P \text{ for some } P \in \mathcal{C}\} \] 이제 \(M\)이 \(H\) 위의 matching이라는 것을 증명하겠습니다. 만약 \(M\)이 matching이 아니라면, \(M\)에 속한 두 간선이 하나의 정점을 공유하고 있을 것입니다. 일반성을 잃지 않고 \( (u^\ell, v^r_1), (u^\ell, v^r_2) \in M \)이라고 하겠습니다.(반대의 경우는 비슷하게 증명하면 됩니다.) 그러려면 \( \langle u, r_1 \rangle \in P_1\)과 \( \langle u, r_2 \rangle \in P_2 \)를 만족하는 \( P_1, P_2 \in \mathcal{C} \)가 존재해야 합니다. 일단 두 간선 모두 \(u\)에서 나가는 간선이므로 \( P_1 \neq P_2 \)라는 사실을 알 수 있습니다. 하지만 그러면 \(\mathcal{C}\)의 서로 다른 두 경로가 \(u\)를 공유하게 되므로 \( \mathcal{C} \)가 path cover라는 사실에 모순이 됩니다.
이제 \( |M| = n - |\mathcal{C}| \)임을 보이면 증명이 완성됩니다. \(\mathcal{C}\)의 모든 경로의 간선들에 대해 \(M\)이 만들어졌으므로, \( |M| = \sum_{P \in \mathcal{C}} |P| \)라는 사실을 알 수 있습니다. 그러면 정리 1을 통해 원하는 결과를 이끌어낼 수 있습니다. □

위 정리를 쉽게 풀어 쓰면, \(G\)에 크기가 작은 path cover가 존재하면 \(H\)에는 크기가 큰 matching이 존재한다는 것입니다. 이제 그 반대도 성립하는지를 따져보도록 하겠습니다. 만약 \(G\)에 순환이 없다면, \(H\)에 크기가 큰 matching이 존재한다는 사실이 \(G\)에 크기가 작은 path cover가 존재한다는 사실을 암시합니다.
정리 3. Matching to path cover
순환이 없는 \(G\)에 대해, \(H\)의 한 maximum matching을 \(M\)이라고 했을 때, \(G\)에는 크기가 \(n - |M|\)인 path cover가 존재한다.
[증명] 먼저 \(M\)에서 \(G\)의 path cover \(\mathcal{C}\)를 하나 만들어 보겠습니다. (나중에 간단하게 증명하겠지만) \(G\)에 순환이 없기 때문에 분명 \(v^r_1 \in R\)이 \(M\)에 대해 exposed한 \(v_1 \in V\)가 존재할 것입니다. 만약 \(v^\ell_1 \in L \)도 \(M\)에 대해 exposed하다면 \( \langle v_1 \rangle \)을 \( \mathcal{C} \)에 넣습니다. 그렇지 않고 \(v^\ell_1\)이 matched라면, 그 짝 \(v^r_2 \in R\)을 찾습니다. 만약 \( v^\ell_2 \)가 exposed라면 이제는 \( \langle v_1, v_2 \rangle \)를 \( \mathcal{C} \)에 넣습니다. 그렇지 않으면 이 작업을 계속 반복하여 \( v^r_t \)가 matched이고 \(v^\ell_t\)가 exposed인 \(v_t\)를 찾은 후, \( \langle v_1, \cdots, v_t \rangle \)를 \(\mathcal{C}\)에 넣습니다. 이후 여기서 고려된 정점들과 \(M\)의 간선들은 모두 고려 대상에서 제외한 다음, 이를 반복합니다. 다시 말해, 상기한 일련의 작업을 \[ \mathcal{C} := \{ \langle v_1, \cdots, v_t \rangle : (v^\ell_i, v^r_{i + 1}) \in M \text{ } \forall i = 1, \cdots, t - 1, \text{ & } v^r_1, v^\ell_t \text{ are exposed} \} \]으로 간단히 표현할 수 있겠습니다.
이제 \(\mathcal{C}\)가 path cover임을 보이도록 하겠습니다. 먼저 \( v^r_1 \in R \)이 \(M\)에 대해 exposed한 \(v\)가 존재하는지부터 따져보겠습니다. 그래야 \(\mathcal{C}\)의 경로를 만들 수 있을테니 말이죠. 만약 그러한 \(v\)가 존재하지 않는다면, 분명 \( (v^\ell_1, v^r_2), (v^\ell_2, v^r_3), \cdots, (v^\ell_t, v^r_1) \in M \)을 모두 만족하는 정점의 나열 \( v^\ell_1, v^r_2, v^\ell_2, \cdots, v^\ell_t, v^r_1 \)이 존재할 것입니다. 이를 \(G\)에 그대로 \( \langle v_1, v_2, \cdots, v_t, v_1 \rangle \)과 같이 옮기면 순환이 됩니다. 이는 원래 \(G\)에 순환이 없다는 가정에 모순이 됩니다.
\(H\)에서 \(|L| = |R|\)이고, \(R\)에는 \(M\)에 대해 exposed한 정점이 하나는 존재한다고 방금 증명하였으므로, 분명 \(L\)에도 하나는 존재할 것이고 \(v^\ell_t\)가 exposed인 \(v_t\)를 찾는 것도 항상 가능합니다. 또한, \(L\)과 \(R\) 각각에서 고려된 정점들의 개수는 동일하며, 제외 후 남은 \(M\)은 여전히 \(H\)의 남은 부분의 matching을 이루게 되므로 이 작업을 계속 반복할 수 있습니다.
\( \langle u, v \rangle \in A \)인 경우에 \( (u^\ell, v^r) \in E \)였으므로, 모든 \( \langle v_1, \cdots, v_t \rangle \)는 \(G\)의 경로를 이루게 됩니다. 또한 \(M\)이 matching이었으며, 한 번 고려된 정점은 다시는 고려되지 않는다는 점을 통해서 이렇게 얻은 경로들이 서로 정점을 공유하지 않는다는 사실도 쉽게 보일 수 있습니다. 마지막으로 더이상 \(H\)에 남은 정점이 없을 때까지 위 작업을 반복할 것이므로 경로들이 모든 정점을 덮을 것이라는 것도 알 수 있습니다. 따라서 \( \mathcal{C} \)는 \(G\)의 한 path cover입니다.
마지막으로 \( |C| = n - |M| \)임을 보이도록 하죠. 임의의 \(P = \langle v_1, \cdots, v_t \rangle \in \mathcal{C}\)에 대해, \( (v^\ell_1, v^r_2), \cdots, (v^\ell_{t - 1}, v^r_t) \in M \)이고, 모든 경로는 서로 간선을 공유하지 않으므로 \( |M| = \sum_{ P \in \mathcal{C}} |P| \)임을 알 수 있습니다. 따라서, 정리 1에 의해 원하는 바를 얻을 수 있습니다. □
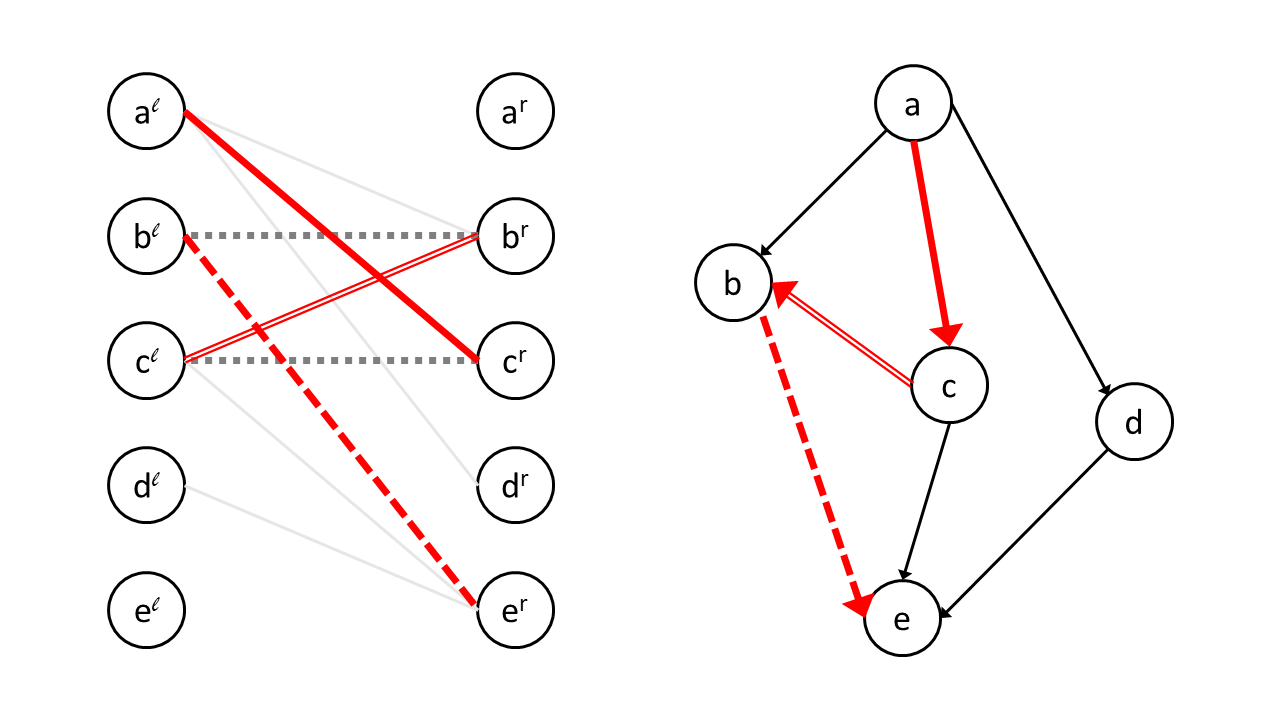
정리 2와 3을 통해서 우리는 다음과 같은 알고리즘을 얻을 수 있습니다.
알고리즘 1. An efficient algorithm for the minimum path cover in DAGs
입력: 순환이 없는 방향 그래프 \(G = (V, A)\)
출력: path cover
- 상술한 대로 auxiliary bipartite graph \(H = (L \cup R, E)\)를 만든다.
- \(H\)에서 maximum matching \(M\)을 구한다.
- 정리 3에서 제시된 방법을 통해 \(\mathcal{C}\)를 만든다.
- \(\mathcal{C}\)를 반환한다.
[증명] 정리 2를 통해서 \(G\) 위의 임의의 path cover \(\mathcal{C}^\prime\)에 대해, \( |M| \geq n - |\mathcal{C}^\prime| \)임을 알 수 있고, 이를 정리하면 \[ n - |M| \leq |\mathcal{C}^\prime| \]을 얻을 수 있습니다. 정리 3을 통해 \[ |\mathcal{C}| = n - |M| \]을 유도할 수 있으며, 두 부등식을 조합하면 \( \mathcal{C} \)가 minimum path cover임을 증명할 수 있습니다.
단계 2는 다항 시간에 해결하는 알고리즘이 잘 알려져 있습니다. 단계 1과 3을 다항 시간에 동작하도록 구현하는 것도 그렇게 어려운 일은 아닙니다. 따라서 이 알고리즘 전체도 다항 시간에 동작합니다. □
이것으로 minimum path cover problem에 대한 포스트를 마무리하도록 하겠습니다. 간략히 정리하면, 일반적인 방향 그래프가 주어진 경우에 minimum path cover problem을 다항 시간에 해결하는 것은 쉽지 않지만, 순환이 없는 그래프가 입력으로 주어지면 bipartite matching으로 환원하여 다항 시간에 해결할 수 있습니다.
그러면 일반적인 그래프에서는 어떤 부분이 망가지게 되는 것일까요? 앞에서 구체적으로 밝히지는 않았으나 정리 2는 일반적인 그래프에서도 여전히 성립합니다. 문제는 정리 3에서 발생합니다. 바로, 순환이 생기기 때문이죠. 만약 임의의 그래프에서 단순 경로가 아니라 정점을 공유하지 않는 순환으로 모든 정점을 덮고 있다면(다시 말해, cycle cover) 이는 \(H\)에서 perfect matching을 이루게 됩니다. 어떤 path cover를 갖고 와도 위와 같은 방식으로는 \(H\)에 perfect matching을 만들 수 없기에 알고리즘이 망가지게 되는 것이죠.
그렇다면 임의의 그래프에 대해서 위 알고리즘이 개수가 가장 작은 cycle cover를 반환할까요? 그것도 아닙니다. 아무 cycle cover든지 모두 \(H\)에서 perfect matching을 이룰 것이므로 이를 분리하는 것은 완전 다른 문제가 됩니다. 실지로 개수가 가장 작은 cycle cover를 구하는 문제도 NP-난해합니다. 바로 어떤 그래프에 모든 정점을 정확히 한 번씩 경유하는 순환이 존재하는지를 판별하는 문제가 NP-완전하기 때문입니다. 본문에서 보인 방식과 비슷하게 증명할 수 있습니다.
이것으로 모두 마치겠습니다. 재미있는 문제를 소개해준 형님한테 다시 한 번 고맙다는 말을 전합니다. 잘못된 점이 있거나 이해가 잘 되지 않는 부분이 있다면 알려주시기 바랍니다. 읽어 주셔서 고맙습니다.